Multiplication et Simplification

[Visiteuse]

Bonjour !
C'est la première fois que je viens sur un forum d'aide pour les devoirs, alors merci de dire si mes explications ne sont pas assez explicite.

Nous voyons en se moment en cours les fractions (Multiplication, addition, etc..). c'est relativement simple, jusque ce que l'on aborde les simplification des fractions. Alors là, c'est simple, je n'es absolument rien compris. Il y a une histoire de décomposé la multiplication, puis de barrer les chiffres qui ont je-ne-sais-quoi en commun.. Je bloque complètement.
Si quelqu'un pouvait m'aider, je suis comme ça en se moment -> :mur:

Merci d'avance.

[CompanionCube]

Bonjour !
C'est la première fois que je viens sur un forum d'aide pour les devoirs, alors merci de dire si mes explications ne sont pas assez explicite.

Nous voyons en se moment en cours les fractions (Multiplication, addition, etc..). c'est relativement simple, jusque ce que l'on aborde les simplification des fractions. Alors là, c'est simple, je n'es absolument rien compris. Il y a une histoire de décomposé la multiplication, puis de barrer les chiffres qui ont je-ne-sais-quoi en commun.. Je bloque complètement.
Si quelqu'un pouvait m'aider, je suis comme ça en se moment -> :mur:

Merci d'avance.

Salut,

Si j'ai bien compris c'est la simplification qui te pose problème..

Tu sais que a/b*c/d = (a*c)/(b*d)

Alors si par exemple tu as la fraction (a*b)/(a*c)
C'est égal = a/a * b/c
a/a est égal à 1
Donc (a*b)/(a*c)=1*b/c=b/c

Par exemple 28/21
Tu remarque que ça fait (7*4)/(7*3)=7/7 * 4/3 = 1*4/3 = 4/3

[Hossam]

Bienvenue à toi, bon, supposons a:b, Nous avons, a = c x d x e, et b= d x f x p x e
cela est équivalent à dire que a:b = ( c x d x e ): ( d x f x p x e) , une fois arrivée à cette étape là, tu barres comme tu as dit les chiffres en commun et dans ce cas on a que le e :), j'espere avoir passer le message et bonne chance.

[C.Ret]

Hossame et CompagnionCube vos expliations sont bien à propos. Mais je crains qu'elles ne soient pas à la portée de Visiteuse.
Au primaire et collège, il me semble que l'on voit les fraction avant les expressions litérales.


Alors, j'ai bien peur que les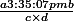 n'aident pas beaucoup notre amie Visiteuse.



Prenons une fraction avec des nombres, je suis sûr que cela sera bien plus simple ! :zen:

Par exemple :


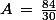
Il est clair que cette fraction n'est pas irréductible, on peut la simplifier.

Par exemple, on voit que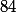 et 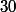sont tous les deux pairs. On peux donc certainement simplifier par deux.

En eff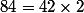et, et .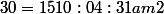

D'où on peut écrire la fraction comme cela :


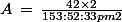
Visiteuse a déjà vu les produits de matrice, donc, elle sait que :


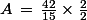
Or, la fraction égale 1, on a donc :

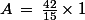
Soit


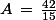
On vient juste de simplifier la fraction par deux. Je l'ai fait en plusieurs lignes pour bien décomposer les étapes.

Mais, avec l'habitude, on peux aller plus vite. Il suffit d'avoir remarqué que l'on a fait disparaitre un facteur 2 en haut (au numérateur de A) et en bas (au dénominateur de A).

Pour marquer que l'on simplifie par 2, les calculeux ont pris l'habitude de barrer le nombre en haut et en bas. Ainsi, pour aller plus vite on écrira :




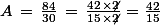
Bon. ?

Mais, la fraction telle que ci-dessus n'est pas encore complètement simplifiée. En effet, on sait que 42 et 15 sont tous les deux dans la table de multiplication de 3. On peut donc encore simplifier par 3.

Je laisse Visiteuse faire le calcul elle-même.

Quand on est fort en math, on prend vite l'habitude de décomposer les nombres en facteurs.
Ainsi, certains auraient directement posé la simplification de de cette façon:



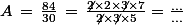
Je laisse Visiteuse compléter le résultat et nous donner la fraction réduite (c'est à dire que l'on ne peut plus simplifier).

[Kikoo <3 Bieber]

Vous vous escrimez joyeusement mes amis !
Mais visiteuse n'est, et son profil le confirme, qu'une visiteuse... :zen:

[C.Ret]

:doh:
Comment va-t-on faire ?
Que va-t-on devenir ?
:eek:
Elle ne reviendra plus ?
:cry:

[Hossam]

Non elle est partie pour de bon cette fois :s