Représentation ensemble de définition
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Jacky22
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Sep 2012, 11:03
-
 par Jacky22 » 19 Aoû 2013, 14:49
par Jacky22 » 19 Aoû 2013, 14:49
Bonjour à tous,
Voici mon problème :
Représenter l'ensemble
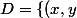\in\mathbb{R}^{2}\quad/\quad x^{2}+y^{2}\leq\quad |x|\})
L'idée que j'ai eu c'est de passer en coordonnées polaires:
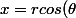)
et
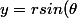)
, ce qui revient à
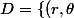\in(\mathbb{R},[0,2\pi])\quad/\quad |r|\leq\quad cos(\theta)\})
Donc D correspond au disque unité, vu que

?
Je ne suis vraiment pas convaincu, merci pour toute aide.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 19 Aoû 2013, 15:06
par adrien69 » 19 Aoû 2013, 15:06
Bah non, le point (0,1) n'y est pas par exemple. Ça fait plutôt une sorte de signe infini rempli.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 19 Aoû 2013, 15:17
par adrien69 » 19 Aoû 2013, 15:17
En fait tu t'es fait avoir, ici le polaire c'est nul. On fait le bord :
Quand x est positif,
x²+y²-x=0 <=> (x-1/2)²+y²=(1/2)², c'est l'équation d'un cercle de rayon 1/2 de centre (1/2,0).
Dans le cas où x est négatif, c'est son symétrique par rapport à l'axe des ordonnées.
-
Jacky22
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Sep 2012, 11:03
-
 par Jacky22 » 19 Aoû 2013, 15:27
par Jacky22 » 19 Aoû 2013, 15:27
Ah la la, je me suis encore pris le choux pour rien.
Merci beaucoup adrien69.
-
Elizabet
- Membre Naturel
- Messages: 54
- Enregistré le: 19 Aoû 2013, 15:16
-
 par Elizabet » 19 Aoû 2013, 18:08
par Elizabet » 19 Aoû 2013, 18:08
Et
l'outil wolfram t'aide à tracer n'importe quelle courbe : c'est un double disque plein d'axe de symétrie
=(O,\mathbf{j}))
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 20 Aoû 2013, 21:40
par deltab » 20 Aoû 2013, 21:40
Bonsoir
[quote="Jacky22"]
L'idée que j'ai eu c'est de passer en coordonnées polaires:
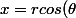)
et
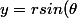)
, ce qui revient à
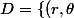\in(\mathbb{R},[0,2\pi])\quad/\quad |r|\leq\quad cos(\theta)\})
/QUOTE]
Tu devrais trouver
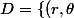\in \mathbb{R} \times [0,2\pi] \quad/\quad 0 \le r \leq\quad)

)

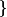
et l'on voit bien apparaitre une symétrie par rapport à l'axe des y.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 20 Aoû 2013, 21:47
par adrien69 » 20 Aoû 2013, 21:47
C'est résolu Deltab, le polaire c'était une mauvaise idée.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 20 Aoû 2013, 22:10
par deltab » 20 Aoû 2013, 22:10
Bonsoir
adrien69 a écrit:C'est résolu Deltab, le polaire c'était une mauvaise idée.
Je sais. C'était pour corriger l'erreur qu'a faite Jacky22 en passant en coordonnées polaires (omission de la valeur absolue dans
)
et valeur absolue superflue dans

.
La dite erreur n'a pas été relevée dans les précédents messages.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 20 Aoû 2013, 22:20
par adrien69 » 20 Aoû 2013, 22:20
Ah oui c'est vrai, j'avais pas tilté, je l'avais lu comme tu l'as écrit.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités