Géométrie complexe

[Imod]

J'ai une solution très courte qui doit être à peu près équivalente à celle de jlb .

Dans un parallélogramme la somme des carrés des diagonales est égale à la somme des carrés des côtés : .
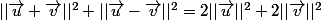
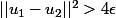
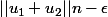
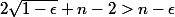
Après on suppose par l'absurde que alors donc ce qui est impossible .

Imod

[jlb]

Du coup, dans les conditions de l'énoncé ( je pense que c'est la valeur que j'ai trouvé mais je n'en sais rien à vrai dire), peut-on trouver un majorant "optimal" pour m et donnés?
Après, je ne sais même pas si ma question a du sens ou même un quelconque intérêt!!!

[adrien69]

Euuuuuh... C'est le théorème de l'inégalité triangulaire forte ?

[jlb]

Euuuuuh... C'est le théorème de l'inégalité triangulaire forte ?

Salut Adrien, jamais entendu parler de ce théorème. Aurais-tu as une référence? Merci.

[adrien69]

Euh... Il est utilisé dans la preuve du théorème de Pringsheim, mais mis à part ça...
Bah c'est simple, si tu as des nombres complexes sommés, il n'y a égalité dans l'inégalité triangulaire que si tous tes nombres sont sur la même demi-droite c'est à dire ont même argument modulo 2pi).

[jlb]

Ok, merci!! A+.

[Imod]

Sauf erreur il me semble que

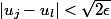
Imod

[Imod]

La démonstration n'est pas très formelle mais la différence maximale est atteinte pour la configuration suivante :



On applique Al-Kashi deux fois et on obtient :
2cos(â)=2-x² et 2(m-1)cos(â)=(m-1)(2e-2)+2e-e² c'est à dire que :
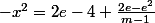
Ce qui nous donne pour y la deuxième diagonale du losange de sommet A et de côté 1 :
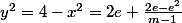
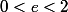
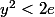
Comme ( sinon aucun intérêt ) , alors et .

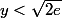
Imod

[adrien69]

Je suis à peu près sûr que c'est

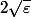
[Imod]

Il y avait bien une erreur dans mon calcul :hum:

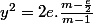
, ce qui donne et on a bien la borne annoncée : .

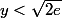
Imod

[Imod]

Il y avait bien une erreur dans mon calcul :hum:

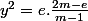
, ce qui donne et on a bien la borne annoncée : .

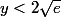
Imod