Equation différentielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
JPhi
- Membre Naturel
- Messages: 14
- Enregistré le: 19 Jan 2006, 21:43
-
par JPhi » 28 Aoû 2006, 15:59
Bonjour,
Voici l'énoncé d'un exo :
 = e^{ - \pi t^2 })
Calculer la fonction F(v) la dérivée de la transformée de Fourier de f :
 = \frac{{\partial F}}{{\partial \nu }})
D'apres mon cours :
^p f(t)-TF->\frac{{\partial ^p F}}{{\partial \nu ^p }})
donc :
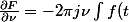.e^{ - 2\pi j\nu } dt} = - 2\pi j\nu .F(\nu ))
Ensuite, en déduire une équation défférentielle qui donne une solution F(v) de la Forme
 = Ae^{ - \pi \nu ^2 })
et que A=1:
Donc on a :
 + 2\pi j\nu .F(\nu ) = 0)
La solution générale est normalement :
 = C.e^{ - \int {2\pi j\nu } } = C.e^{ - \pi jv^2 })
Et puis là je trouve pas :hein:
Merci d'avance pour votre aide.
a+
JP
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
par nox » 29 Aoû 2006, 08:53
qu'est ce que tu ne trouves pas ? :hein:
il n'y a plus rien à faire la non ?
-
JPhi
- Membre Naturel
- Messages: 14
- Enregistré le: 19 Jan 2006, 21:43
-
par JPhi » 29 Aoû 2006, 09:29
Mon
)
a un
en trop et je ne vois pas comment montrer que A est forcément égale à 1.
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
par nox » 29 Aoû 2006, 09:41
JPhi a écrit:D'apres mon cours :
^p f(t))
euh mais cette formule c'est pas la transformée de fourier de la dérivée plutot? :hein:
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
par nox » 29 Aoû 2006, 09:44
y a pas confusion entre transformée de fourier de la dérivée et dérivée de la transformée de fourier au début ? :hein:
-
JPhi
- Membre Naturel
- Messages: 14
- Enregistré le: 19 Jan 2006, 21:43
-
par JPhi » 29 Aoû 2006, 15:25
On me demande bien de calculer la dérivée de la TF.
Tu vois une inversion possible dans les calculs ?
J'ai trouvé un exo équivalent avec la même equa diff qui débouchait aussi sur
avec A=1: et parlait d'equa diff à variable séparable. :hum:
Je vais continuer à chercher dans ce sens.
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
par nox » 29 Aoû 2006, 16:04
ba moi j'ai vu que :
)' = \int{ixe^{itx}f(x)dx)
(donc la dérivée de la transformée de Fourier, que tu recherches) et que TF(f') = ixTF(f) (donc la transformée de Fourier de la dérivée)
-
xon
- Membre Relatif
- Messages: 100
- Enregistré le: 24 Aoû 2006, 14:57
-
par xon » 29 Aoû 2006, 17:31
Il y a effectivement une erreur pour l'ordre de dérivation
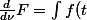.\frac{d}{d\nu}e^{-2\pi j\nu t}dt=\int e^{-\pi t^{2}}.(-2\pi jt).e^{-2\pi j\nu t}dt=-2\pi j\int te^{-\pi t^{2}}.e^{-2\pi j\nu t}dt)
et vu comme c'est ecrit tu as très envie de faire une intégration par parties en integrant
.
et là çà devrait mieux se passer
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
par nox » 29 Aoû 2006, 17:58
il cartonne ce bon vieux xon surtout quand il est d'accord avec moi
PS : tu pourrais répondre aux mails ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
