Question bete
6 messages
- Page 1 sur 1
par Cactuss » 20 Juil 2013, 18:15
Archytas a écrit:
Merci,
J'ai donc trouvé que cela donnait -1.
Peut on retrouver avec cela :
sachant que
par Olympus » 21 Juil 2013, 00:26
Salut !
Regarde le développement en série de Fourier de la fonction
-périodique qui à 
dans 
associe 
.
Regarde le développement en série de Fourier de la fonction
par deltab » 21 Juil 2013, 00:53
Bonsoir
Indépendamment de la relation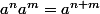
, on pourra remarquer que 
et 
sont de parités opposées au sens il y a un pair et un impair et donc parmi les deux facteurs ^{n-1})
et ^n)
, l'un vaut 1 et l'autre -1, leur produit vaut donc -1.
En ce qui concerne la série^{n-1}}{ n^2})
, (et non k=1) je ne vois comment faire intervenir^{n-1}(-1)^n)
pour calculer sa somme.
la série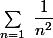
est absolument convergente, on peut séparer les termes d'indice pair et ceux d'indice inpair et on aura:
^{n-1}}{ n^2}=\sum_{n=1}\dfrac{ (-1)^{2n-1}}{ 4n^2}+\sum_{n=0}\dfrac{ (-1)^{2n} }{ (2n+1)^2}=-\sum_{n=1}\dfrac{1}{ (2n)^2}+\sum_{n=0}\dfrac{ 1}{ (2n+1)^2}=\sum_{n=0}\dfrac{ 1}{ (2n+1)^2}-\dfrac{1}{4}\sum_{n=1}\dfrac{1}{ n^2})
De même
^2})
d'où^2}=\sum_{n=1}\ \dfrac{1}{ n^2}-\sum_{n=1}\dfrac{1}{ 4n^2}=(1-\dfrac{1}{4})\sum_{n=1}\ \dfrac{1}{ n^2}=\dfrac{3\pi^2}{24}=\dfrac{\pi^2}{8})
et^{n-1}}{ n^2}=-\sum_{n=1}\dfrac{1}{ (2n)^2}+\sum_{n=0}\dfrac{ 1}{ (2n+1)^2}=\dfrac{\pi^2}{8}-\dfrac{1}{4}\times \dfrac{\pi^2}{6}=\dfrac{\pi^2}{12})
Cactuss a écrit:Merci,
J'ai donc trouvé que cela donnait -1.
Peut on retrouver avec cela :
sachant que
Indépendamment de la relation
En ce qui concerne la série
la série
De même
d'où
et
par Cactuss » 21 Juil 2013, 01:06
Merci Olympus et deltab pour le détails de ta réponse.
J'ai réussi entre temps à trouver la bonne réponse à mon problème.
Une petite faveur à vous demander, est-ce que vous auriez un peu de temps et d'expérience pour m'aider un autre exercice concernant l'étude de série?
Je poste mon problème sur un nouveau topic.
J'ai réussi entre temps à trouver la bonne réponse à mon problème.
Une petite faveur à vous demander, est-ce que vous auriez un peu de temps et d'expérience pour m'aider un autre exercice concernant l'étude de série?
Je poste mon problème sur un nouveau topic.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :