Equa diff partielles

[zonotope]

Bonjour,

est-ce que quelqu'un aurait des références biblio sur la résolution d'équa diff. partielles, ou bien quelques pistes à me donner sur le problème suivant svp ?



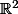
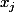
où est une constante, une fonction de dans , la dérivée seconde de par rapport à et la dérivée seconde de par rapport à puis à .

Merci...

[adrien69]

Y a tjr les polys de la FIFMA.

[Pythales]

Bonjour,

est-ce que quelqu'un aurait des références biblio sur la résolution d'équa diff. partielles, ou bien quelques pistes à me donner sur le problème suivant svp ?



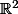
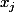
où est une constante, une fonction de dans , la dérivée seconde de par rapport à et la dérivée seconde de par rapport à puis à .

Merci...

Je suppose que tu veux dire que est fonction de
Si oui, c'est facile.

Sinon il y a la solution évidente

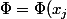[zonotope]

Je suppose que tu veux dire que est fonction de
Si oui, c'est facile.

Sinon il y a la solution évidente

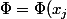Merci Pythales, mais non, on sait juste que sans aucune restriction... Et je voudrais bien-sûr éviter les solutions évidentes... Merci quand même !

[Pythales]

Merci Pythales, mais non, on sait juste que sans aucune restriction... Et je voudrais bien-sûr éviter les solutions évidentes... Merci quand même !

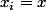
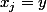
Dans ce cas tu poses (pour simplifier les notations) , et et ton équation devient
qui est une équation linéaire du 1er ordre qu'on sait (?) résoudre.