Distributions
19 messages
- Page 1 sur 1
distributions
Bonjour
j'ai un petit soucis avec un exo sur les distributions:
T'' + 2T' + 2T = Delta(a) Delta => impulsion de dirac
(ou a est un parametre réel)
1)Calculer la reposne implusionnel dans D'+ par la méthode de l'equation différentiel (de fonctions) associée.
Quelqu'un a t-il une solution détaillée ?
(Il le faut pas utiliser Lapalce ni Fourier)
Merci de votre aide
j'ai un petit soucis avec un exo sur les distributions:
T'' + 2T' + 2T = Delta(a) Delta => impulsion de dirac
(ou a est un parametre réel)
1)Calculer la reposne implusionnel dans D'+ par la méthode de l'equation différentiel (de fonctions) associée.
Quelqu'un a t-il une solution détaillée ?
(Il le faut pas utiliser Lapalce ni Fourier)
Merci de votre aide
nekros a écrit:Salut quinto,
Dis-moi, la transformée de Laplace, c'est de la SI ??!
Comment ça s'utilise ?
La transformée de Laplace est un opérateur mathématique.
Il sert entre autre, à transformer une équation différentielle en une équation algébrique. C'est un opérateur continue (pour une certaine norme), donc c'est assez intéressant aussi, parce que si tu deux solutions des équations algébriques que tu as après transformation qui sont très proches, tu sais que les solutions des équations différentielles de départ sont également très proche.
Tape transformée de Laplace (ou de Fourier, c'est presque pareil) sur un moteur de recherche et tu auras quelques applications utiles et quelques informations théoriques intéressantes sur le sujet.
a+
C'est vrai que Laplace s'est vraiment pratique pour ce genre d'equation. Ca evite d'avoir à passer par des fonctions.
Sinon une methode, c'est de dire que ton delta est une liimite de fonction f_n, de résoudre pour ces crénaux. et de faire tendre le crenau vers une impulsion.
Le mieux c'est quand même de rester dans le domaine des distributions, et d'appliquer Laplace. Tu a directement ta réponse spectral, que tu retraduit en déphase et amplification (ou amortissement).
Sinon une methode, c'est de dire que ton delta est une liimite de fonction f_n, de résoudre pour ces crénaux. et de faire tendre le crenau vers une impulsion.
Le mieux c'est quand même de rester dans le domaine des distributions, et d'appliquer Laplace. Tu a directement ta réponse spectral, que tu retraduit en déphase et amplification (ou amortissement).
buzard a écrit:C'est vrai que Laplace s'est vraiment pratique pour ce genre d'equation. Ca evite d'avoir à passer par des fonctions.
Sinon une methode, c'est de dire que ton delta est une liimite de fonction f_n, de résoudre pour ces crénaux. et de faire tendre le crenau vers une impulsion.
Le mieux c'est quand même de rester dans le domaine des distributions, et d'appliquer Laplace. Tu a directement ta réponse spectral, que tu retraduit en déphase et amplification (ou amortissement).
:doh: Je crois que ma maigre contribution sur ce sujet s'arrête là :salut:
A+
Salut,
EDIT : déjà été fait comme l'a dit Sdec25.
Je pense plutôt qu'il faut résoudre l'équadiff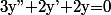 , comme dans ton premier post.
, comme dans ton premier post.
Tu formes d'abord l'équation caractéristique suivante :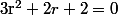
Les racines sont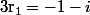 et
et 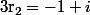
La solution générale de l'équadiff est donc les fonctions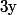 définies par
définies par =exp{-x}(\lambda_1 cos(x)+\lambda_2 sin(x)))
Reste à appliquer les conditions initiales : = 1) et
et  = 0)
Sauf erreurs, on trouve que la solution de l'équadiff vérifiant ces conditions initiale est la fonction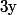 définie par
définie par =exp{-x} sin(x)) .
.
A+
En faite il faut resoudre y'' + 2y + 2 = 0
avec y'(0) = 1 et y(0) = 0
EDIT : déjà été fait comme l'a dit Sdec25.
Je pense plutôt qu'il faut résoudre l'équadiff
Tu formes d'abord l'équation caractéristique suivante :
Les racines sont
La solution générale de l'équadiff est donc les fonctions
Reste à appliquer les conditions initiales :
Sauf erreurs, on trouve que la solution de l'équadiff vérifiant ces conditions initiale est la fonction
A+
niko61 a écrit:le probleme c'est les racines complexes je me souviens plus comment on fait
Tu peux voir ce lien
A+
Sdec25 a écrit:cet exercice a été posté 2 fois (ici)
L'exercice d'origine parlait de l'équadiff T'' + 2T' + 2T=0 et non de T''+2T+2=0
Alors Niko, tu voulais quelle équadiff ? :hum:
A+
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
