bonsoir (2sin n +1)/n² est elle convergente?
j'ai pensé au critere de riemann en multippliant pat n² on trouve que la serie de tterme generale (2sin n +1)/n² est convergente, est-ce bon?
Serie divergente ou convergente?;
3 messages
- Page 1 sur 1
par deltab » 22 Juin 2013, 09:44
Bonjour.
Si vous entendez par critère de Riemman l'étude de
, cette limite n'existe pas pour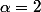 
et +1}{n^2})
. De plus la suite +1}\{n^2}\right))
n'est pas à signe constant. Le critère comparaison (avec use série de Riemann) pour l'étude de la convergence absolue est plus rapide: +1}\{n^2}\right)\right| \le \left(\frac{2\sin(n)+1}{n^2}\right))
Si vous entendez par critère de Riemman l'étude de
kmikazi a écrit:bonsoir (2sin n +1)/n² est elle convergente?
j'ai pensé au critere de riemann en multippliant pat n² on trouve que la serie de tterme generale (2sin n +1)/n² est convergente, est-ce bon?
par deltab » 22 Juin 2013, 09:53
Bonjour.
Si vous entendez par critère de Riemman l'étude de, cette limite n'existe pas pour 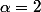et . De plus la suite +1}{n^2}\right))
n'est pas à signe constant. Le critère de comparaison (avec une série de Riemann,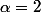
) pour l'étude de la convergence absolue est plus rapide: +1}{n^2}\right| \le \dfrac{3}{n^2})
. On a donc la convergence absolue donc la convergence.
Si vous entendez par critère de Riemman l'étude de
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :