Bonsoir , j'ai une matrice A =
2 1 4
0 1 0
1 1 2
Je dois trouver le polynome caracteristique de A et verifier qu'il est égal a: x^3-5x²+4x
J'ai trouvé trace de a = 5
det(a) = 0
Mais il me manque une donnée la trace de la comatrice.
Pouvez vous m'aider svp.
Matrice besoin d'une explication
6 messages
- Page 1 sur 1
Salut !
Soit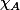 le polynôme caractéristique de
le polynôme caractéristique de  .
.
Calcule=\det(A-XI)) .
.
baba11 a écrit:Bonsoir , j'ai une matrice A =
2 1 4
0 1 0
1 1 2
Je dois trouver le polynome caracteristique de A et verifier qu'il est égal a: x^3-5x²+4x
J'ai trouvé trace de a = 5
det(a) = 0
Mais il me manque une donnée la trace de la comatrice.
Pouvez vous m'aider svp.
Soit
Calcule
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Bonsoir,
la comatrice de A -dite aussi matrice des cofacteurs- est tout simplement la matrice ayant pour composantes ses mineurs (c'est-à-dire les déterminants de ses sous-matrices).
Si on appelle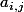 le déterminant de la sous-matrice déduite de A (matrice initiale) en ayant enlevé la i_ème ligne et la j_ème colonne, alors son cofacteur est
le déterminant de la sous-matrice déduite de A (matrice initiale) en ayant enlevé la i_ème ligne et la j_ème colonne, alors son cofacteur est ^{i+j}*a_{i,j})

Avec, dans ton cas :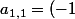^{1+1}*2*\begin{vmatrix} 1 & 0 \\ 1 & 2 \end{vmatrix}=4)
Quant à la trace d'une matrice,, je suppose que tu sais de quoi il s'agit.
la comatrice de A -dite aussi matrice des cofacteurs- est tout simplement la matrice ayant pour composantes ses mineurs (c'est-à-dire les déterminants de ses sous-matrices).
Si on appelle
Avec, dans ton cas :
Quant à la trace d'une matrice,, je suppose que tu sais de quoi il s'agit.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
