Domaine de définition de Ln
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sophie_lee
- Membre Naturel
- Messages: 33
- Enregistré le: 03 Mai 2013, 16:59
-
 par sophie_lee » 13 Juin 2013, 12:59
par sophie_lee » 13 Juin 2013, 12:59
Déterminer l'ensemble de définition de la fonction f
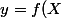 = f(x1;x2) = 1/3 [ln(x1x2+e)^2]^3)
Merci d'avance ! :we: :we:

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 13 Juin 2013, 13:00
par ampholyte » 13 Juin 2013, 13:00
Bonjour,
Tu sais que ln(x) est défini pour x appartenant à ]0; +oo[.
Il te suffit donc d'étudier le signe de x1x2 + e > 0 pour trouver l'ensemble de définition de la fonction f.
-
sophie_lee
- Membre Naturel
- Messages: 33
- Enregistré le: 03 Mai 2013, 16:59
-
 par sophie_lee » 13 Juin 2013, 13:07
par sophie_lee » 13 Juin 2013, 13:07
ampholyte a écrit:Bonjour,
Tu sais que
)
est défini pour x appartenant à

.
Il te suffit donc d'étudier le signe de

> 0 pour trouver l'ensemble de définition de la fonction f.
[CENTER]
 __
__ ____
____ ___
___et
___
?[/CENTER]

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 13 Juin 2013, 13:22
par ampholyte » 13 Juin 2013, 13:22
C'est ça =).
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 13 Juin 2013, 13:58
par Robic » 13 Juin 2013, 13:58
Cela dit, l'argument du logarithme est mis au carré (le carré porte sur l'argument du logarithme, pas sur le logarithme globalement puisqu'il y a une puissance 3 sur le logarithme globalement), donc c'est toujours positif et il faut juste vérifier que ce n'est pas nul.

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 13 Juin 2013, 14:41
par ampholyte » 13 Juin 2013, 14:41
Hum, tu as raison, je suis parti de la fonction f(x1, x2) = 1/3 * [ln(x1x2 - e)²]³ et non de
f(x1, x2) = 1/3 * [ln((x1x2 - e)²)]³ dans ce cas il suffit simplement de vérifier (comme Robic l'a dit) que x1x2 soit différent de e.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 108 invités
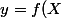 = f(x1;x2) = 1/3 [ln(x1x2+e)^2]^3)
