Équation à deux inconnus

par **sophie_lee** » 12 Juin 2013, 16:15

Bonjour tout le monde, j'ai une équation à deux inconnus que je n'arrive pas à résoudre pouvez vous m'aidez ? Merci d'avance :we:
[CENTER]
4-[(x-1)²+(y+1)²]=0 [/CENTER]

par **Archibald** » 12 Juin 2013, 16:22

Donc, du type

ça ne te dit vraiment rien ?

par **sophie_lee** » 12 Juin 2013, 16:26

Archibald a écrit:Donc, du type

ça ne te dit vraiment rien ?

Malheureusement, ça me dit vraiment rien .. :/
J'ai pensée le résoudre par

ce qui me donne

et

mais ensuite quand je les remplacent, ça me donne pas 0 mais -2 ..

par **sophie_lee** » 12 Juin 2013, 16:30

sophie_lee a écrit:Malheureusement, ça me dit vraiment rien .. :/
J'ai pensée le résoudre par

ce qui me donne
et
mais ensuite quand je les remplacent, ça me donne pas 0 mais -2 ..

Aah non c'est bon j'ai trouvé... C'était pourtant simple, il suffit que je remplace

dans l'équation et je trouve

. Parce qu'avant j'avais posé

par **ampholyte** » 12 Juin 2013, 16:31

Bonjour,

Ici la solution est plutôt une solution "géométrique".

Résoudre y = ax + b pourrait donner :
"droite de coefficient directeur a et d'ordonnée à l'origine b."

par **Archibald** » 12 Juin 2013, 19:03

sophie_lee a écrit:Malheureusement, ça me dit vraiment rien .. :/
J'ai pensée le résoudre par

ce qui me donne
et
mais ensuite quand je les remplacent, ça me donne pas 0 mais -2 ..

tu n'as donc jamais vu l'équation d'un cercle dans le plan ? ce serait alors étrange qu'on te donne à faire cet exercice là.

Tu as donc une équation du type :

qui est en fait l'équation d'un cercle de centre

et de rayon

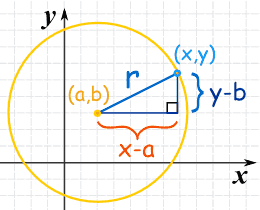
En rouge, quelques couples solutions de ton équation, mais il y a autant de couple solution que de point sur un cercle, c'est-à-dire une infinité.

Équation à deux inconnus

Équation à deux inconnus

Qui est en ligne