Nombres échangeables
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 10 Juin 2013, 15:04
par t.itou29 » 10 Juin 2013, 15:04
Bonjour,
Je n'arrive pas à finir un exercice:
On considère la fonction f de R dans R définie par
=a-\sqrt{x+b})
avec a,b réels.
Deux nombres sont échangeable si f(x)=y et f(y)=x.
Montrer que deux nombres sont échangeables ssi

J'ai trouvé le système suivant:
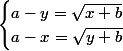
, qui en mettant au carré et en soustrayant implique
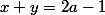
pour

.
Je vois bien que comme

, il faut que

mais je ne sais pas comment le démontrer.
Pouvez-vous m'aider ?
Merci
-
Hypatie
- Membre Naturel
- Messages: 20
- Enregistré le: 09 Juin 2013, 16:30
-
 par Hypatie » 10 Juin 2013, 15:50
par Hypatie » 10 Juin 2013, 15:50
t.itou29 a écrit:Bonjour,
Je n'arrive pas à finir un exercice:
On considère la fonction f de R dans R définie par
=a-\sqrt{x+b})
avec a,b réels.
Deux nombres sont échangeable si f(x)=y et f(y)=x.
Montrer que deux nombres sont échangeables ssi

J'ai trouvé le système suivant:
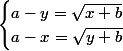
, qui en mettant au carré et en soustrayant implique
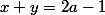
pour

.
Je vois bien que comme

, il faut que

mais je ne sais pas comment le démontrer.
Pouvez-vous m'aider ?
Merci
Bonjour,
il faut utiliser le fait que
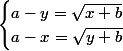
et donc que

A présent à l'aide de
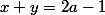
, exprime a en fonction de x et y seulement, en remplaçant dans le système précédent tu devrais pouvoir trouver.
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 10 Juin 2013, 16:47
par t.itou29 » 10 Juin 2013, 16:47
Hypatie a écrit:Bonjour,
il faut utiliser le fait que
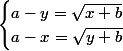
et donc que

A présent à l'aide de
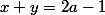
, exprime a en fonction de x et y seulement, en remplaçant dans le système précédent tu devrais pouvoir trouver.
Bonjour,
En remplaçant je tombe sur

, mais je ne vois pas comment isoler le x et le y.
-
Hypatie
- Membre Naturel
- Messages: 20
- Enregistré le: 09 Juin 2013, 16:30
-
 par Hypatie » 10 Juin 2013, 17:52
par Hypatie » 10 Juin 2013, 17:52
t.itou29 a écrit:Bonjour,
En remplaçant je tombe sur

, mais je ne vois pas comment isoler le x et le y.
Il faut plutot faire
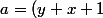/2)
et remplacer a dans

et

Là tu vas avoir une condition sur x-y et y-x
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 10 Juin 2013, 18:09
par t.itou29 » 10 Juin 2013, 18:09
Hypatie a écrit:Il faut plutot faire
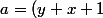/2)
et remplacer a dans

et

Là tu vas avoir une condition sur x-y et y-x
Ok merci , alors

et

qui implique

c'est à dire

, est-ce bon ?
-
Hypatie
- Membre Naturel
- Messages: 20
- Enregistré le: 09 Juin 2013, 16:30
-
 par Hypatie » 10 Juin 2013, 18:24
par Hypatie » 10 Juin 2013, 18:24
t.itou29 a écrit:Ok merci , alors

et

qui implique

c'est à dire

, est-ce bon ?
Attention il y a juste une petite erreur
/2-y = (x-y+1)/2 \ge 0)
donc

de même
/2-x = (y-x+1)/2 \ge 0)
donc

Ainsi

et

d'où

-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 10 Juin 2013, 18:28
par t.itou29 » 10 Juin 2013, 18:28
Hypatie a écrit:Attention il y a juste une petite erreur
/2-y = (x-y+1)/2 \ge 0)
donc

de même
/2-x = (y-x+1)/2 \ge 0)
donc

Ainsi

et

d'où

Ah merci, oui une grosse erreur même !
-
Hypatie
- Membre Naturel
- Messages: 20
- Enregistré le: 09 Juin 2013, 16:30
-
 par Hypatie » 10 Juin 2013, 18:39
par Hypatie » 10 Juin 2013, 18:39
t.itou29 a écrit:Ah merci, oui une grosse erreur même !
Oui c'est sûr c'est faux sinon mais "petite erreur" je trouve ça plus sympa à écrire et à lire!
Sinon pour répondre au merci, ravie de t'avoir aidé!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
