Géométrie analytique et équations paramétriques

[Kael8]

Bonjour,

Je bloque sur l'énoncé suivant:

"Déterminer les coordonnées des points d’intersection de la courbe d’équation
cartésienne x^2 + y^2 + 2x - 4y = 13 avec celle dont une équation cartésienne est donnée par
x^2 + y^2 -6x + 4y + 11 = 0"

J'ai commencé par transformer les équations cartésiennes en:
(x+1)^2 + (y-2)^2 = 18 pour le premier cercle
(x-3)^2 + (y+2)^2 = 2 pour le second.. Mais ça ne me menait à rien.

J'ai alors trouvé les équations paramétriques de ces deux cercles:
Pour le premier: x = -1 + 3rac(2) cos(teta) et y = 2 + 3rac(2) sin(teta)
Pour le second: x = 3 + rac(2) cos (mu) et y = -2 + rac(2) sin (mu)


Je sais que la réponse est (2 ; -1) mais je n'arrive pas à déterminer comment faire.

Quelqu'un pourrait-il m'aider?

Merci d'avance,

Kael.

[Manny06]

Bonjour,

Je bloque sur l'énoncé suivant:

"Déterminer les coordonnées des points d’intersection de la courbe d’équation
cartésienne x^2 + y^2 + 2x - 4y = 13 avec celle dont une équation cartésienne est donnée par
x^2 + y^2 -6x + 4y + 11 = 0"

J'ai commencé par transformer les équations cartésiennes en:
(x+1)^2 + (y-2)^2 = 18 pour le premier cercle
(x-3)^2 + (y+2)^2 = 2 pour le second.. Mais ça ne me menait à rien.

J'ai alors trouvé les équations paramétriques de ces deux cercles:
Pour le premier: x = -1 + 3rac(2) cos(teta) et y = 2 + 3rac(2) sin(teta)
Pour le second: x = 3 + rac(2) cos (mu) et y = -2 + rac(2) sin (mu)


Je sais que la réponse est (2 ; -1) mais je n'arrive pas à déterminer comment faire.

Quelqu'un pourrait-il m'aider?

Merci d'avance,

Kael.

tu fais la différence des deux équations de départ,tu obtiendras l'équation d'une droite ensuite tu cherches l'intersection de cette droite avec l'un des cercles (ce qui revient à resoudre le système)

[capitaine nuggets]

Méthode classique :

Posons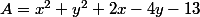 et .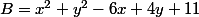
Les points d'intersections de ces deux courbes sont solutions du système :



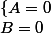
Or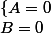 équivaut à 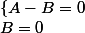donc je te laisse poursuivre :++:

[Black Jack]

x^2 + y^2 + 2x - 4y = 13
x^2 + y^2 -6x + 4y + 11 = 0

Par soustraction membre à membre des 2 équations précédentes, on arrive rapidement à
x = y + 3

Résultat remis dans une des équations de départ :
(y+3)² + y² + 2(y+3) - 4y = 13
développer et résoudre ...
On a une seule solution double qui est y = -1

et on calcule le x correspondant par x = y+3 = ...

:zen:

[Kael8]

Un grand merci!