Petite démonstration : x^y=y^x.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kinoa
- Membre Naturel
- Messages: 78
- Enregistré le: 07 Fév 2013, 13:36
-
 par Kinoa » 02 Juin 2013, 20:28
par Kinoa » 02 Juin 2013, 20:28
Bonsoir tout le monde,
Je bloque sur l'exercice suivant et donc sollicite votre aide
 On me demande de démontrer que l'équation :
On me demande de démontrer que l'équation :
x^y=y^x définit y comme fonction de x, aux alentours du point (2,4).
---
Je ne vois pas trop quoi utiliser pour démontrer.. Quelqu'un aurait-il une piste par hasard ?
Merci d'avance pour votre aide

.
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 02 Juin 2013, 20:48
par Archibald » 02 Juin 2013, 20:48
Bonsoir,
1) intuitivement, pour toi, quels seraient les couples solutions évidentes à cette équation ?
2) utiliser le népérien, puis étudie les variations de la nouvelle expression
-
Kinoa
- Membre Naturel
- Messages: 78
- Enregistré le: 07 Fév 2013, 13:36
-
 par Kinoa » 02 Juin 2013, 20:53
par Kinoa » 02 Juin 2013, 20:53
Hello :)
1/ Intuitivement, (2,4) et (4,2).
2/ Pour le népérien ok, j'arrive à ln(x)/x = ln(y)/y, mais pour la suite, je bloque, je ne vois pas vraiment quelle piste prendre..
Dois-je par exemple définir : y = f(x) = ln(x)/x et étudier cette fonction ?
Merci bien
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 02 Juin 2013, 21:29
par Archibald » 02 Juin 2013, 21:29
1) ok, mais il y a un couple beaucoup plus évident que ça. Le plus trivial après le (0,0)
2) Tout à fait. Il faut étudier ses variations en gardant en tête que ton équation de départ est symétrique
-
Kinoa
- Membre Naturel
- Messages: 78
- Enregistré le: 07 Fév 2013, 13:36
-
 par Kinoa » 02 Juin 2013, 21:31
par Kinoa » 02 Juin 2013, 21:31
Ok je vois ! Je vais y réfléchir encore un peu alors :)
Je reposte ici très bientôt pour te tenir au courant.
Merci beaucoup pour le coup de main :)
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 02 Juin 2013, 23:58
par Robic » 02 Juin 2013, 23:58
La question n'est pas de résoudre cette équation mais de démontrer qu'il existe une fonction f telle que y=f(x) au voisinage de (2, 4). Donc est-ce qu'il ne faut pas plutôt utiliser le théorème des fonctions implicites ?
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 03 Juin 2013, 09:49
par adrien69 » 03 Juin 2013, 09:49
Quand Archibald dit d'étudier les variations c'est ce qu'il suggère ;)
-
Kinoa
- Membre Naturel
- Messages: 78
- Enregistré le: 07 Fév 2013, 13:36
-
 par Kinoa » 03 Juin 2013, 21:14
par Kinoa » 03 Juin 2013, 21:14
Ah ce n'est pas une étude de fonction dont on parle alors ? (Variations, etc..).
Pour ce qui est du théorème des fonctions implicites, je ne connais pas pour le moment, de quoi s'agit t'il ?
Merci d'avance. :)
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 03 Juin 2013, 22:50
par mrif » 03 Juin 2013, 22:50
Kinoa a écrit:Ah ce n'est pas une étude de fonction dont on parle alors ? (Variations, etc..).
Pour ce qui est du théorème des fonctions implicites, je ne connais pas pour le moment, de quoi s'agit t'il ?
Merci d'avance.

On étudie la fonction f définie par f(x) = ln(x)/x.
Posons I = ]0;e] et J = [e;+l'infini[
f est croissante sur I et décroissante sur J. Soit g la fonction réciproque de la restriction de f à J.
f(I) = f(J) = ]0;1/e]. L'application h définie de I dans J par h(x) = g(f(x)) = g(ln(x)/x) est bien définie sur I, un voisinage de x = 2, dans J, un voisinage de y = 4, et on a bien h(2) = 4 et f(h(x)) = f(x).
Redit correctionf(I) et f(J) ne sont pas égaux comme affirmé plus haut car f(I) = ]-l'infini;1/e] et f(J) = ]0;1/e] et du coup I n'est plus le voisinage de 2 qui convient. Mais l'idée reste valable à savoir f/I et f/J sont 2 fonctions continues monotones donc inversibles, de réciproques continues, et on prendra comme voisinage de 2 l'intervalle
^{-1}(f/J)^{-1}f(J))
.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 01 Juil 2013, 19:22
par deltab » 01 Juil 2013, 19:22
Bonjour à tous.
Kinoa: Pour ce qui est du théorème des fonctions implicites, je ne connais pas pour le moment, de quoi s'agit t'il ?
De l'aveu de Kinoa, il ne peut montrer l'existence de la fonction f à l'aide du théorème des fonctions explicites, mais que peut-être on peut explicitement exprimer y en fonction de x.
Kinoa:Pour le népérien ok, j'arrive à ln(x)/x = ln(y)/y
En posant
=\dfrac{\ln(x)}{x})
et
=\dfrac{\ln(y)}{y})
, alors
=\int f(x)dx=\int \dfrac{\ln(x)}{x}dx)
et
=\int g(y)dy=\int \dfrac{\ln(y)}{y}dy=\int \dfrac{\ln(x)}{x}dx)
On en déduit donc
=F(x)+C=\int \dfrac{\ln(x)}{x}dx=\ln^2(x)+C)
d'où
>+C\ln^2(x)+C et |\ln(x)|=\sqrt{\ln^2(x)>+C})
.
En
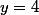
,

, on aura alors |\ln(y)|=\ln(y).
on doit aussi avoir en (2,4) :
=4\ln^2(2)=\ln^2(2)+C)
d'où
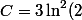)
donc
=\sqrt{\ln^2(x)+3\ln^2(2)})
et finalement
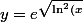+3\ln^2(2)}})
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 02 Juil 2013, 12:06
par adrien69 » 02 Juil 2013, 12:06
Y a des /2 qui traînent normalement mais ça m'a l'air pas mal !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 02 Juil 2013, 12:59
par Doraki » 02 Juil 2013, 12:59
J'trouve que c'est du grand n'importe quoi.
On cherche une fonction continue y(x) telle que x^y(x) = y(x)^x et y(2)=4, définie autour de 2.
L'équation se réécrit, en posant g(z) = ln(z)/z, g(x) = g(y(x)).
On a bien g(2) = g(4) = ln(2)/2.
g'(z) est du même signe que (1/z)*z - ln(z)*1 = 1-ln(z), donc g est strictement croissante de ]0;e[ sur ]-l'infini ; 1/e[, atteint son maximum 1/e en z=e, puis est strictement décroissante de ]e;+l'infini[ sur ]0;1/e[.
De plus, g(1)=0, donc g restreinte à ]1;e] est une bijection croissante continue vers ]0;1/e],
et g restreinte à [e;+l'infini[ est une bijection décroissante continue vers ]0;1/e]
Maintenant il suffit de prendre y(x) = (g|[e;+l'infini[)^-1 (g|]1;e](x)), et ça définit une bijection décroissante continue de ]1;e] sur ]0;1/e], et il est trivial de vérifier que g(x) = g(y(x)) et que c'est la seule possible qui soit définie sur ]1;e].
(bon en fait j'ai juste recopié mrif)
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 02 Juil 2013, 17:14
par deltab » 02 Juil 2013, 17:14
Bonjour à tous.
adrien69 a écrit:Y a des /2 qui traînent normalement mais ça m'a l'air pas mal !
Je reprend pour correction des facteurs 1/2 qui manquaient et les erreurs du copier-coller.
On en déduit donc
=F(x)+C=\int \dfrac{\ln(x)}{x}dx=)

+C_1)
d'où:

=)

+C_1)
En posant

, on aura alors
|=\sqrt{\ln^2(x)+C})
.
En
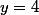
,

, on aura alors au voisinage de
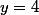
:
|=\ln(y))
.
on doit aussi avoir en
)
:
=4\ln^2(2)=\ln^2(2)+C)
d'où
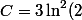)
donc
=\sqrt{\ln^2(x)+3\ln^2(2)})
et finalement
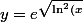+3\ln^2(2)}})
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 02 Juil 2013, 17:23
par Doraki » 02 Juil 2013, 17:23
Ton truc est faux à la première ligne.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 02 Juil 2013, 17:51
par deltab » 02 Juil 2013, 17:51
Doraki a écrit:Ton truc est faux à la première ligne.
Mon dernier post fait suite et corrige les erreurs que j'avais faites lors de mon 1er post. Pour les notations, j'ai repris celles que j'avais déjà utilisées.
et je ne vois toujours pas où est l'erreur que j'ai faite à la première ligne. Peux-tu me l'expliquer?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 02 Juil 2013, 18:04
par Doraki » 02 Juil 2013, 18:04
Permets-moi de réutiliser ton raisonnement dans un autre cadre :
Montrer que x² = y² définit y come fonction de x autour du point (-1,1).
Je copie-colle ton truc :
En posant f(x) = x² et g(y) = y² (j'imagine que tu voulais dire g(y) et pas g(x)), alors :
x^3/3 = F(x) = intégrale de f(x)dx = intégrale de x²dx, et
y^3/3 = G(y) = intégrale de g(y)dy = intégrale de y²dy = intégrale de x²dx
On en déduit donc G(y) = F(x) + C = x^3/3 + C, d'où y^3/3 = x^3/3 + C
comme on part du point(-1,1), on obtient 1/3 = -1/3 + C donc C = 2/3, et donc y = (x^3 + 2)^(1/3).
Alors qu'on était bien sûr sensé trouver y= -x
y devrait être le nom d'une fonction et tu devrais toujours écrire y(x) pour parler de "la valeur de y correspondant à telle valeur de x".
Et aussi tu devrais donner des bornes à tes intégrales, et donner des noms de variables différents à des variables différentes.
ln²(u) = F(u) = intégrale de 1 à u de ln(x)/x dx = intégrale de 1 à u de ln(y(x))/y(x) dx, et là tu ne peux plus avancer.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 02 Juil 2013, 18:54
par deltab » 02 Juil 2013, 18:54
Avant tout bonjour.
@Doraki
Je comprend maintenant où était mon erreurr.
J'avais }{x}=\frac{\ln(y)}{y}) et non
et non }{x}dx=\frac{\ln(y)}{y}dy) .
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
