Algèbre linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 10 Fév 2013, 11:50
par Kikoo <3 Bieber » 10 Fév 2013, 11:50
Salut à vous,
J'aimerais savoir pourquoi les seuls s.e.v du

-espace vectoriel

sont

et lui-même.
Merci pour toute réponse !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Fév 2013, 12:21
par Doraki » 10 Fév 2013, 12:21
La preuve s'écrit toute seule. T'as essayé de le démontrer ?
Tu peux aussi expliciter une base de K et voir que K est un K-ev de dimension 1.
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
 par Archytas » 10 Fév 2013, 12:51
par Archytas » 10 Fév 2013, 12:51
Kikoo <3 Bieber a écrit:Salut à vous,
J'aimerais savoir pourquoi les seuls s.e.v du

-espace vectoriel

sont

et lui-même.
Merci pour toute réponse !
Pour R tu écris la définition avec les combinaison linéaires d'un espace vectoriel engendré par {0,k} (k non nul) et puis... pareil pour C ^^ !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 10 Fév 2013, 13:19
par Kikoo <3 Bieber » 10 Fév 2013, 13:19
Salut vous deux !
Je crois que j'ai finalement une démo pour K=R ou C
On sait que {0} et K sont deux s.e.v de K grâce à leur stabilité par + et ., ainsi que par le fait qu'ils contiennent le vecteur nul {0}.
Montrons que de manière réciproque, ils sont les seuls à convenir.
Si F est réduit au vecteur nul, nous avons fini une partie de la démo.
Maintenant, supposons que F n'est pas égal au vecteur nul. Alors il existe un vecteur x différent du vecteur nul appartenant à F.
Soit y un vecteur de K. Alors y=(y/x)*x qui appartient à F car y/x est un scalaire (raisonnement par stabilité). Alors y appartient aussi à F : K est inclu dans F.
Or nous avions supposé que F est inclu dans K, donc par double inclusion, F=K
Alors les seuls s.e.v de K sont {0} et K.
Merci :)
-
raph107
- Membre Relatif
- Messages: 205
- Enregistré le: 17 Sep 2005, 08:53
-
 par raph107 » 10 Fév 2013, 15:03
par raph107 » 10 Fév 2013, 15:03
Kikoo <3 Bieber a écrit:Salut vous deux !
Je crois que j'ai finalement une démo pour K=R ou C
On sait que {0} et K sont deux s.e.v de K grâce à leur stabilité par + et ., ainsi que par le fait qu'ils contiennent le vecteur nul {0}.
Montrons que de manière réciproque, ils sont les seuls à convenir.
Si F est réduit au vecteur nul, nous avons fini une partie de la démo.
Maintenant, supposons que F n'est pas égal au vecteur nul. Alors il existe un vecteur x différent du vecteur nul appartenant à F.
Soit y un vecteur de K. Alors y=(y/x)*x qui appartient à F car y/x est un scalaire (raisonnement par stabilité). Alors y appartient aussi à F : K est inclu dans F.
Or nous avions supposé que F est inclu dans K, donc par double inclusion, F=K
Alors les seuls s.e.v de K sont {0} et K.
Merci

Doraki a proposé une démonstration beaucoup plus simple qui marche pour tout corps K:
K est un K-ev de dimension 1, donc les sous espaces vectoriels sont soit de dimension 0, soit de dimension 1, donc soit {0} soit K.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 13 Fév 2013, 23:01
par Kikoo <3 Bieber » 13 Fév 2013, 23:01
raph107 a écrit:Doraki a proposé une démonstration beaucoup plus simple qui marche pour tout corps K:
K est un K-ev de dimension 1, donc les sous espaces vectoriels sont soit de dimension 0, soit de dimension 1, donc soit {0} soit K.
Je ne suis pas encore sur le chapitre à propos des dimensions finies

Mais cela viendra.
Merci.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 09 Mar 2013, 21:56
par Kikoo <3 Bieber » 09 Mar 2013, 21:56
Bonsoir,
Je travaille dans l'espace

, R-ev des fonctions polynômiales de R dans R de degré égal à moins l'infini (fonction nulle) ou inférieur ou égal à n. Pour

, on note l'application
=\Delta(P))
avec
(x)=P(x+1)-P(x))
On vérifie ensuite le long de l'exo que pour

,
(0)=k!\delta_{j,k})
avec

le symbole de Kronecker.
J'en viens à la difficulté :
Soit

, écrit dans la base
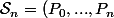=(1,x,x(x-1),...,x(x-1)...(x-n+1)))
avec l'expression :
[CENTER]

[/CENTER]
Il me faut montrer que
(0)}{k!})
Et je ne vois pas vraiment comment en arriver à quelque chose comme ça.
Merci de m'apporter un peu d'aide !

-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 09 Mar 2013, 22:23
par Joker62 » 09 Mar 2013, 22:23
Hello !
Appliquer Delta^j sur ton polynôme P et applique en 0
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 09 Mar 2013, 23:05
par Kikoo <3 Bieber » 09 Mar 2013, 23:05
Merci beaucoup Joker, je vais voir ce que cela donne !
C'était tout bête !
J'ai
(x)=\sum_{k=0}^n a_k\Delta^j(P_k)(x))
En évaluant en x=0, j'obtiens :
(0)=\sum_{k=0}^n a_k\Delta^j(P_k)(0)=a_j j!)
d'où la réponse.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 10 Mar 2013, 00:39
par Joker62 » 10 Mar 2013, 00:39
Et ça ressemble drôlement à des formules de Taylor !
D'ailleurs Delta, ça ressemble drôlement à un opérateur de dérivation
D'ailleurs c'est de la dérivation discrète !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 10 Mar 2013, 18:13
par Kikoo <3 Bieber » 10 Mar 2013, 18:13
Joli, je ne savais pas cela !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 24 Mai 2013, 20:38
par Kikoo <3 Bieber » 24 Mai 2013, 20:38
Bonsoir,
Je m'aperçois un peu tardivement que j'ai du mal à effectuer le déterminant d'une n*n tridiagonale.
Soit
 = \begin{vmatrix}1-2X & X & \cdots &0 &0 \\ X& 1-2X & \cdots & 0 & 0\\ \vdots& \vdots & \ddots& \vdots &\vdots \\ 0 & 0&\cdots & 1-2X & X\\ 0& 0 &\cdots & X &1-2X \end{vmatrix})
J'obtiens la relation de récurrence suivante en décomposant le déterminant selon la règle du cofacteur :
=(1-2X)\Delta_{n-1}\(X\)-X\begin{vmatrix}X & X & \cdots &0 &0 \\ 0& 1-2X & \cdots & 0 & 0\\ \vdots& \vdots & \ddots& \vdots &\vdots \\ 0 & 0&\cdots & 1-2X & X\\ 0& 0 &\cdots & X &1-2X \end{vmatrix})
et je n'arrive pas à l'étape suivante
=(1-2X)\Delta_{n-1}\(X\)-X^2\Delta_{n-2}\(X\))
car je ne comprends tout simplement pas quelle opération (opération élémentaire sur des colonnes ou des lignes ?) on a pu effectuer.
Merci beaucoup !
PS : J'ai trouvé en réfléchissant un peu. On développe à nouveau selon la première ligne en faisant sortir X. Merci quand-même !
PPS : Dans le cas où le discriminant du polynôme caractéristique associé est non nul, quelqu'un pourrait confirmer la réponse que j'obtiens ?
=\frac{1}{\sqrt{1-4X}} \(-\(\frac{1-2X-\sqrt{1-4X}}{2}\)^n+\(\frac{1-2X+\sqrt{1-4X}}{2}\)^n\))
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 28 Mai 2013, 17:15
par Kikoo <3 Bieber » 28 Mai 2013, 17:15
Salut !
J'aimerais montrer qu'une application est une symétrie de M2(C) (cette application transforme une matrice du-dit espace en une autre matrice de cet espace).
Pouvez-vous m'orienter sur une démarche à adopter s'il-vous-plait ?
Merci !
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 28 Mai 2013, 17:44
par Skullkid » 28 Mai 2013, 17:44
Salut, après avoir montré que ton application f est bien linéaire, essaye de calculer f^2 (le but du jeu étant de montrer que f^2 = id).
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 28 Mai 2013, 17:55
par Kikoo <3 Bieber » 28 Mai 2013, 17:55
Skullkid a écrit:Salut, après avoir montré que ton application f est bien linéaire, essaye de calculer f^2 (le but du jeu étant de montrer que f^2 = id).
Merci bien Skullkid !

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités