Méthode de pénalisation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 27 Mai 2013, 12:36
par egan » 27 Mai 2013, 12:36
Salut tout le monde,
Je bloque sur un problème de pénalisation en optimisation. Voici mon problème.
Je considère les fonctions
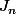
définies sur

par:
 = 2x^2 + 3xy + 2y^2 + n(x+0.5)^2(y+0.5)^2)
On sait que chaque
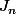
admet un minimum sur

. On le note
)
.
Le but est de montrer que
)
converge vers
)
.
J'ai réussi à montrer que soit

, soit

convergeait vers -0.5 mais je suis bloqué pour conclure.
Avez-vous des idées ?
@+ Boris.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 27 Mai 2013, 12:56
par Doraki » 27 Mai 2013, 12:56
egan a écrit:On sait que chaque
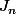
admet un minimum sur

. On le note
)
.
Il se passe quoi si le minimum est atteint pour plusieurs valeurs ?
-
skwouale
- Membre Naturel
- Messages: 40
- Enregistré le: 05 Avr 2013, 13:00
-
 par skwouale » 27 Mai 2013, 12:56
par skwouale » 27 Mai 2013, 12:56
[quote="egan"]Salut tout le monde,
polynome de degré 2, y a pas moyen de calculer le minimum (xn,yn) en fonction de n directement ?
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 27 Mai 2013, 21:36
par egan » 27 Mai 2013, 21:36
Le polynôme est de degré 4.
T'as raison Doraki, c'est louche. J'imagine que si la méthode est bien faite, à partir d'un certains rang il n'y a qu'un seul minimum.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Mai 2013, 08:11
par Doraki » 28 Mai 2013, 08:11
Ben les minimums de (x+1/2)²(y+1/2)² sont (-1/2,3/8) et (3/8,-1/2), et quand n tend vers l'infini, c'est vers eux que tendent les minimums de Jn.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités