Démonstration propriétés probabilités
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
adriadeus
- Membre Naturel
- Messages: 35
- Enregistré le: 24 Juil 2012, 11:39
-
par adriadeus » 26 Mai 2013, 14:25
Bonjour,
Je dois démontrer 8 propriétés, en partant des axiomes de Kolmogorov et en me basant sur celles déjà démontrées. J'ai réussi à démontrer les 4 premières :
1)
=1-P(A))
2)
\leq 1)
3)
=0)
4)
=P(A)+P(B)-P(A\cap B))
).
Il me reste donc à démontrer les 4 dernières :
5)
=1-P(A\cap B))
6)
=1-P(A\cup B))
7)
=P(A\cap B)+P(A\cap \overline{B}))
8) si
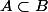
, alors
\leq P(B))
.
Je n'arrive pas à démontrer ces quatre dernières propriétés. Elles sont logiques, mais formellement je ne sais pas comment faire. Quelqu'un connaît-il les démonstrations? Merci d'avance pour vos réponses.
-
LaCoc6nl
- Membre Naturel
- Messages: 90
- Enregistré le: 29 Mar 2013, 19:06
-
par LaCoc6nl » 26 Mai 2013, 16:48
adriadeus a écrit:Il me reste donc à démontrer les 4 dernières :
5)
6)
7)
8) si
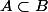
, alors
.
Je n'arrive pas à démontrer ces quatre dernières propriétés. Elles sont logiques, mais formellement je ne sais pas comment faire. Quelqu'un connaît-il les démonstrations? Merci d'avance pour vos réponses.
La 5) se déduit de la 1) et de la 4) car :
=P(\overline{A})+P(\overline{B})-P(\overline{A}\cap \overline{B}))
=
 + 1-P(B) - P(\overline{A}\cap \overline{B}))
=
 + 1 - P(A\cap B) - P(\overline{A\cup B}))
=
 + 1 - P(A\cap B) - P(\overline{A\cup B}))
=
)
. La 6) se déduit en passant la 5) au complémentaire, la 7) et 8) en dessins...
-
adriadeus
- Membre Naturel
- Messages: 35
- Enregistré le: 24 Juil 2012, 11:39
-
par adriadeus » 26 Mai 2013, 17:14
D'accord merci beaucoup! c'était surtout la 5 qui me posait problème.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
