Algèbre linéaire et matrice
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 22 Mai 2013, 16:54
par Maxmau » 22 Mai 2013, 16:54
lau852 a écrit:j'ai pas reussit a bien formater le matrice sur le forum j'ai donc publier l'image de ce que j'ai fait par écrit
scan
tu n'as pas écrit la matrice M
-
lau852
- Membre Naturel
- Messages: 22
- Enregistré le: 14 Jan 2011, 23:00
-
 par lau852 » 22 Mai 2013, 18:31
par lau852 » 22 Mai 2013, 18:31
la matrice M est sur le première ligne (0,1) est sur la deuxieme (-1,0) donc
scan2
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 22 Mai 2013, 19:00
par Maxmau » 22 Mai 2013, 19:00
lau852 a écrit:la matrice M est sur le première ligne (0,1) est sur la deuxieme (-1,0) donc
scan2
OK..................................................
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 22 Mai 2013, 23:34
par adrien69 » 22 Mai 2013, 23:34
De mon point de vue lau582 n'a rien compris. Va falloir réexpliquer. Je ferai ça demain si j'ai le temps.
-
lau852
- Membre Naturel
- Messages: 22
- Enregistré le: 14 Jan 2011, 23:00
-
 par lau852 » 24 Mai 2013, 21:33
par lau852 » 24 Mai 2013, 21:33
Maxmau : merci. et pour l'implication inverse en supposant que n soit paire je prend une matrice 2n*2n je prend une matrice et je montre qu'il existe un endomorphisme dont le carré est -Ide.
adrien69 : c'est pas comme ça qu'il fallait faire ?

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 25 Mai 2013, 03:42
par alm » 25 Mai 2013, 03:42
Salut
S'il existe
)
tel que
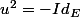
alors on a :
= \det(-Id)=(-1)^n \det(Id)=(-1)^n)
, donc
^n=(\det u)^2 \geq 0)
, par suite
^n=1)
et

est pair.
Réciproque:
Par récurrence sur

avec
=2m)
et

.
Si
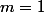
soit
)
une base de

et soit
)
tel que
=e_2)
et
=-e_1)
.
Démontre que
=-e_1)
et
=-e_2)
et conclut.
Soit

tel que la propriété à démontrer vrai pour tout espace vectoriel réel de dimension

.
Soit

un espace vectoriele réel de dimesion

et soit

un plan vectoriel de

et

un supplémentaire de

Par hypothése de récurence il existe
)
et
)
tel que
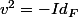
et
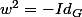
.
Soit
)
tel que
 = v(p(x)) + w(q(x)))
pour tout

avec :

la projection de

sur

parallélement à


la projection de

sur

parallélement à

Prouve que
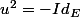 Indications :
Indications : Essayer de comprendre pourquoi on a ce qui suit :
)=v(x)\\ q(v(x))=0\right.)
et
)=w(x)\\ p(w(x))=0\right.)
puis appliquer cela pour prouver que
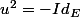
-
lau852
- Membre Naturel
- Messages: 22
- Enregistré le: 14 Jan 2011, 23:00
-
 par lau852 » 26 Mai 2013, 10:33
par lau852 » 26 Mai 2013, 10:33
MOHAMED_AIT_LH a écrit:Salut
S'il existe
)
tel que
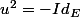
alors on a :
= \det(-Id)=(-1)^n \det(Id)=(-1)^n)
, donc
^n=(\det u)^2 \geq 0)
, par suite
^n=1)
et

est pair.
Réciproque:
Par récurrence sur

avec
=2m)
et

.
Si
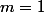
soit
)
une base de

et soit
)
tel que
=e_2)
et
=-e_1)
.
Démontre que
=-e_1)
et
=-e_2)
et conclut.
Soit

tel que la propriété à démontrer vrai pour tout espace vectoriel réel de dimension

.
Soit

un espace vectoriele réel de dimesion

et soit

un plan vectoriel de

et

un supplémentaire de

Par hypothése de récurence il existe
)
et
)
tel que
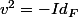
et
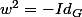
.
Soit
)
tel que
 = v(p(x)) + w(q(x)))
pour tout

avec :

la projection de

sur

parallélement à


la projection de

sur

parallélement à

Prouve que
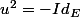 Indications :
Indications : Essayer de comprendre pourquoi on a ce qui suit :
)=v(x)\\ q(v(x))=0\right.)
et
)=w(x)\\ p(w(x))=0\right.)
puis appliquer cela pour prouver que
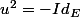
j'ai pas trop compris les 2 phrases suivantes.

la projection de

sur

parallélement à


la projection de

sur

parallélement à

Démontre que
=-e_1)
et
=-e_2)
et conclut. en sachant que
)
=
))
il faut que je trouve l'uimage de u et que je montre qu'on ait
)
=
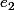
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 26 Mai 2013, 11:17
par adrien69 » 26 Mai 2013, 11:17
Non, ton énoncé n'encourage à utiliser les matrices qu'à la question c), il fallait donc faire comme Mohamed.
-
lau852
- Membre Naturel
- Messages: 22
- Enregistré le: 14 Jan 2011, 23:00
-
 par lau852 » 26 Mai 2013, 11:26
par lau852 » 26 Mai 2013, 11:26
adrien69 a écrit:Non, ton énoncé n'encourage à utiliser les matrices qu'à la question c), il fallait donc faire comme Mohamed.
ok je vais essayer d'utiliser la méthode de mohamed.
-
lau852
- Membre Naturel
- Messages: 22
- Enregistré le: 14 Jan 2011, 23:00
-
 par lau852 » 26 Mai 2013, 13:10
par lau852 » 26 Mai 2013, 13:10
alors j'ai calculer u²(e1) = uou(e1) = u(e2) = -e1
puis u²(e2) = uou(e2)= u(-e1) = -e2 puisque u(e1) = u(e2) équivaut a u(-e1) = u(-e2).
je peut en conclure que la proposition est vrai pour m = 1, si n = 2 ( qui est paire ) il existe un endomorphisme donc le carré est - 1

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 26 Mai 2013, 19:49
par alm » 26 Mai 2013, 19:49
Salut:
Tu part de l'expression
=v(p(x)) + w(q(x)))
, pour tout

et tu l'utilises pour calculer
)
. Tu vas trouver:
=-x)
si tu tiens compte de l'indication que j'avais donné en haut. Comme ça tu aura prouvé que
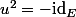
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
tel que
alors on a :
, donc
, par suite
et
est pair.
avec
et
.
soit
une base de
et soit
tel que
et
.
et
et conclut.
tel que la propriété à démontrer vrai pour tout espace vectoriel réel de dimension
.
un espace vectoriele réel de dimesion
et soit
un plan vectoriel de
et
un supplémentaire de

et
tel que
et
.
tel que
pour tout
avec :
la projection de
sur
parallélement à

la projection de
sur
parallélement à
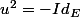
et
)=w(x)\\ p(w(x))=0\right.)