Deux equations differentielles(1er et 2eme ordre)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Yozamu
- Membre Relatif
- Messages: 223
- Enregistré le: 15 Sep 2012, 13:00
-
 par Yozamu » 22 Mai 2013, 19:56
par Yozamu » 22 Mai 2013, 19:56
Bonsoir.
J'essaye de résoudre deux équations différentielles, mais je suis bloqué dans chacune à des endroits différents:
Pour la premiere, l'expression est la suivante:
)y'+(sin(x))y=\frac{(2+cos(x))^2}{\sqrt{1+x^2}})
Je suis déjà bloqué à l'EDL1H, puisque je ne parviens pas à faire la primitive de
}{2+cos(x)})
Concernant la deuxieme, j'ai un petit peu plus avancé, l'expression est:
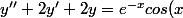)
J'ai abouti à
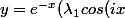+\lambda_{2}sin(ix)))
Mais je ne sais plus comment faire pour finir la résolution
Merci d'avance
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 22 Mai 2013, 20:43
par mr_pyer » 22 Mai 2013, 20:43
Qu'appelles-tu EDL1H ?
Sinon pour la primitive de
}{2+\cos(x)})
tu peux par exemple faire le changement de variable
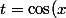)
...
-
Yozamu
- Membre Relatif
- Messages: 223
- Enregistré le: 15 Sep 2012, 13:00
-
 par Yozamu » 22 Mai 2013, 20:55
par Yozamu » 22 Mai 2013, 20:55
J'appelle EDL1H l'équation différentielle linéaire du premier ordre homogène, donc sans second membre.
Pour la primitive je vois, le résultat est-il -ln|2+t| ? (par ailleurs, je ne sais plus s'il faut mettre +c quand on cherche la solution générale de EDL1H, de meme pour la valeur absolue, je ne sais pas si on peut s'en dispenser)
Donc la solution serait y=k.(2+t) (avec ou sans valeur absolue... ?)
Je ne pense jamais à toutes ces méthodes pour trouver les primitives... J'essaye de retenir globalement les "primitives usuelles", mais je ne sais jamais quand faire une IPP ou un changement de variable... Hormis l'entrainement, y a-t-il des astuces permettant de savoir quelle méthode utiliser selon les cas ?
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 22 Mai 2013, 21:09
par mr_pyer » 22 Mai 2013, 21:09
Yozamu a écrit:J'appelle EDL1H l'équation différentielle linéaire du premier ordre homogène, donc sans second membre.
Ok merci j'ai toujours du mal avec les abréviations

Pour la primitive je vois, le résultat est-il -ln|2+t| ?
Attention à ne pas oublier à remplacer t par cos(x).
Je ne pense jamais à toutes ces méthodes pour trouver les primitives...
Ici les règles de BIOCHE s'appliquent par exemple.
(par ailleurs, je ne sais plus s'il faut mettre +c quand on cherche la solution générale de EDL1H, de meme pour la valeur absolue, je ne sais pas si on peut s'en dispenser)
En fait tu peux choisir

comme tu veux (on choisit donc 0) puisqu'il va intervenir dans l'exponentielle mais que tu vas la multiplier par une constante pour avoir toutes les solutions (je ne sais pas si je suis très clair là...).
Sinon la valeur absolue peut disparaître puisque 2+cos(x) > 0.
-
Yozamu
- Membre Relatif
- Messages: 223
- Enregistré le: 15 Sep 2012, 13:00
-
 par Yozamu » 22 Mai 2013, 21:23
par Yozamu » 22 Mai 2013, 21:23
D'accord, merci beaucoup, et effectivement je n'avais pas remplacé!
EDIT: Par contre, je ne parviens toujours pas à resoudre l'equation du second ordre..
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 22 Mai 2013, 22:07
par mr_pyer » 22 Mai 2013, 22:07
Dans ta solution homogène tu as ajouté un i par mégarde...
Ensuite il faut faire varier les constantes
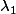
et
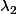
...
-
Yozamu
- Membre Relatif
- Messages: 223
- Enregistré le: 15 Sep 2012, 13:00
-
 par Yozamu » 22 Mai 2013, 22:10
par Yozamu » 22 Mai 2013, 22:10
Oui effectivement je m'en suis rendu compte en recopiant le début au propre et j'avais enlevé les i en recopiant.
Par contre comment ça faire varier les constantes ? Je me souviens être tombé sur un exo comme ça vers le début de l'année mais j'avais déjà pas réussi la premiere fois, donc je connais toujours pas la méthode pour aller plus loin dans la résolution
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 22 Mai 2013, 22:36
par mr_pyer » 22 Mai 2013, 22:36
Là c'est un peu technique :
On peut se contenter de faire varier une constante, par exemple chercher la solution générale de la forme
=\lambda(x)\times e^{-x}\cos(x))
.
Sinon le problème est équivalent à :
=AY(x)+B(x))
avec
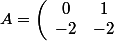)
,
=\left(\begin{array}{c}0\\e^{-x}cos(x)\end{array}\right))
et
=\binom{y(x)}{y'(x)})
.
Il faut alors trouver les fonctions

et

telles que
Y_1(x)+b'(x)Y_2(x) = \left(\begin{array}{c}0\\e^{-x}cos(x)\end{array}\right))
où
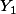
et
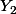
sont deux solutions indépendantes de l'équation homogène (par ex.
=\binom{e^{-x}\cos(x)}{(e^{-x}cos(x))'}\:\:\begin{array}{l}\leftarrow\: y_1(x)\\ \leftarrow\:y_1'(x)\end{array})
).
Edit : Je viens de me rendre compte que je disais de faire varier
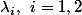
alors que là j'ai fait varier

et

...
Edit2 : Correction d'une erreur grossière.
Edit3 : Mise en forme.
-
Yozamu
- Membre Relatif
- Messages: 223
- Enregistré le: 15 Sep 2012, 13:00
-
 par Yozamu » 23 Mai 2013, 07:02
par Yozamu » 23 Mai 2013, 07:02
Effectivement, c'est assez technique...
Je suis désolé, mais je ne comprends pas du tout
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
