Limite et sup

[dias65]

bonjour,
j'ai besoin d'aide pour cette questio
soit g une fonction définie sur ]0;+infini[ ds R tel que lim g(t)=0 qd x tends vers 0+
Montrer que lim sup valeurabsolue(g(t)) pour t dans [x,2x] = 0 qd x tand vers 0+
merci.

[adrien69]

Salut,
Quantifie. Après ça tombe comme un fruit mûr.

[BorisBob]

bonjour,
j'ai besoin d'aide pour cette questio
soit g une fonction définie sur ]0;+infini[ ds R tel que lim g(t)=0 qd x tends vers 0+
Montrer que lim sup valeurabsolue(g(t)) pour t dans [x,2x] = 0 qd x tand vers 0+
merci.

Soit e > 0.
Comme , il existe z > 0 tel que pour tout t dans ]0 ; z[ on a : |g(t)| 0, il existe w > 0 tel que pour x dans ]0 ; w[
c'est-à-dire :

[adrien69]

BorisBob, ça ne peut qu'être faux ce que tu viens d'écrire. Tu viens de prouver que toute fonction continue en un point y est dérivable. Par exemple d'après ce que tu viens d'écrire, 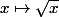est continue en 0...
Faut pas essayer de tout ramener à des exos qu'on a déjà traités.
(Et faut pas non plus balancer des solutions toutes cuites aux gens, c'est contre-productif)


Bon tu as édité, donc pour ce qui est de "c'est faux", je retire, ça a l'air bon (même si c'est compliqué pour un truc aussi simple). Mais ma remarque entre parenthèses est toujours valable.

[BorisBob]

Désolé, je n'ai plus pensé qu'il fallait simplement donner des pistes