Bonjour
Voici Un exercice "classique" de dérivabilité qui me laisse perplexe.
Soit f une fonction définie sur un intervalle contenant 0, et continue en 0.
On suppose que (x->0)lim (f(2x) - f(x))/x admet une limite réelle en 0.
Il faut montrer que f est dérivable en 0.
Merci de toute l'aide qui pourra m'être apporté.
Pb de dérivabilité
10 messages
- Page 1 sur 1
par Archibald » 21 Mai 2013, 13:08
Bonjour,
il faut partir de l'expression d'une fonction dérivable en un point.
 \ = \ \lim_{x \to x_0} \frac{f(x_0)-f(x)}{x_0-x})
il faut partir de l'expression d'une fonction dérivable en un point.
par BorisBob » 21 Mai 2013, 19:38
Je crois avoir trouvé. Indiquer moi svp si mon explication se tient. Posons :  - f(X)}{X}\ = \ \ l)
On montre :
1) Pour tout k entier naturel :-f(\frac{x}{2^k^+^1})}{x} \ = \ \frac{l}{2^k^+^1})
(par changement de variable 
)
2) Pour tout n entier naturel :-f(\frac{x}{2^n^+^1})}{x} \ = \ l*(1 - \frac{1}{2^n^+^1}))
(par sommation du 1) de k = 0 à n)
3) Pour x non nul : - f(0)}{x} \ = \ 0)
(par continuité de f en 0)
4)
Soit e>0.
Pour x non nul et n entier on a : - f(0)}{x} - l | [TEX]n_1)
on a : A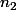 
on a : C 0 tel que pour x vérifiant |x| < z et x non nul on a : B < 
Ainsi : - f(0)}{x}\ = \ \ l)
, c'est-à-dire f dérivable en 0 avec  = l.)
On montre :
1) Pour tout k entier naturel :
2) Pour tout n entier naturel :
3) Pour x non nul :
4)
Soit e>0.
Pour x non nul et n entier on a :
Ainsi :
par adrien69 » 21 Mai 2013, 19:57
C'est presque bon. J'allais publier ma réponse mais tu m'as grillé. En fait ici n1 et n2 dépendent de x, et ça pose problème. Et si tu fixes d'abord x ça posera aussi problème parce que x dépendra alors de n.
Le problème est donc d'avoir une convergence uniforme ou une continuité uniforme à un endroit donné. Et en fait on l'a vu qu'on a la continuité en 0, donc sur un petit intervalle fermé autour de 0 ce qui permet d'appliquer le théorème de Heine (le théorème le plus important qu'on voie avant le bac+3, mis à part celui de convergence dominée, qui n'est par contre pas prouvé). Je te laisse conclure en sachant ça.
Le problème est donc d'avoir une convergence uniforme ou une continuité uniforme à un endroit donné. Et en fait on l'a vu qu'on a la continuité en 0, donc sur un petit intervalle fermé autour de 0 ce qui permet d'appliquer le théorème de Heine (le théorème le plus important qu'on voie avant le bac+3, mis à part celui de convergence dominée, qui n'est par contre pas prouvé). Je te laisse conclure en sachant ça.
par BorisBob » 21 Mai 2013, 21:57
Je vois mon erreur, mais je ne vois pas comment me servir de l'uniforme continuité. Pourrais-tu détailler ?
par adrien69 » 21 Mai 2013, 23:10
Je suis sur mon portable donc bof, mais il faut t'en servir pour mettre tes quantificateurs dans le bon ordre à ton 2)
Je pourrai détailler demain soir.
Je pourrai détailler demain soir.
par BorisBob » 28 Mai 2013, 17:59
adrien69 a écrit:Je suis sur mon portable donc bof, mais il faut t'en servir pour mettre tes quantificateurs dans le bon ordre à ton 2)
Je pourrai détailler demain soir.
Bonsoir,
J'aimerais si possible que l'on me détaille comment utiliser l'uniforme continuité car vraiment je n'arrive pas à m'en servir. De plus je me pose les questions suivantes :
Soit f une fonction définie sur D , avec a dans D.
Est-il vrai que : SI f continue en a suivant D, Alors il existe K compact de D contenant a tel que f continue en a suivant K ?
Dans l'affirmative j'aimerais bien une démo, et dans la négative un contre exemple.
Merci.
par adrien69 » 30 Mai 2013, 10:26
Je déménageais, je t'avais oublié désolé.
Alors le principe c'est que si tu prends un point a où f est continue et si tu prends un point b suffisamment proche de a (à une distance inférieure au éta/2 de ta définition quantifiée de la continuité et si tu prends un point x à une distance d'au plus éta/2 de a, x et b seront à une distance de moins d'éta/2 et |f(x)-f(b)|<|f(x)-f(a)|+f(a)-f(b)|<2epsilon
Alors le principe c'est que si tu prends un point a où f est continue et si tu prends un point b suffisamment proche de a (à une distance inférieure au éta/2 de ta définition quantifiée de la continuité et si tu prends un point x à une distance d'au plus éta/2 de a, x et b seront à une distance de moins d'éta/2 et |f(x)-f(b)|<|f(x)-f(a)|+f(a)-f(b)|<2epsilon
par chan79 » 31 Mai 2013, 09:42
Bonjour
Je propose cette démonstration (à vérifier car pas trop sûr ...)
on pose-f(x)}{x}-l=m(x))
soit=f(x)+x\,l+x\,m(x)\)
égalité 1
la limite de m(x) quand x tend vers 0 étant 0.
soit n un entier fixé
D'après l'égalité 1, on a les égalités:
=f(\fra{x}{2})+\fra{x}{2}\,l+\fra{x}{2}\,m( \fra{x}{2} ))
=f(\fra{x}{2^2})+\fra{x}{2^2}\,l+\fra{x}{2^2}\,m( \fra{x}{2^2} ))
=f(\fra{x}{2^3})+\fra{x}{2^3}\,l+ \fra{x}{2^3} \,m(\fra{x}{2^3}))
=f(\fra{x}{2^4})+\fra{x}{2^4}\,l+ \fra{x}{2^4} \,m(\fra{x}{2^4}))
.....
.....
=f(\fra{x}{2^n})+\fra{x}{2^n}\,l+ \fra{x}{2^n} \,m(\fra{x}{2^n}))
En additionnant membre à membre:
=f(\fra{x}{2^n})+ x\,l (\fra{1}{2} + \fra{1}{2^2} + \fra{1}{2^3} + \fra{1}{2^4}+ ...+\fra{1}{2^n})+\fra{x}{2}\,m( \fra{x}{2} ) + \fra{x}{2^2}\,m( \fra{x}{2^2} ) + \fra{x}{2^3}\,m( \fra{x}{2^3} ) + ... +\fra{x}{2^n}\,m( \fra{x}{2^n} ))
Comme la limite de m(x) quand x tend vers 0 est 0, soit un nombre
; il existe 
tel que:
si x appartient à I=[-,] alors |m(x)|<
on suppose donc que
appartient à I.
Tous les)
ci-dessus sont majorés par .
donc
-f(\fra{x}{2^n})- x\,l (\fra{1}{2} + \fra{1}{2^2} + \fra{1}{2^3} + \fra{1}{2^4}+ ...+\fra{1}{2^n})|< \epsilon \, |x (\fra{1}{2} + \fra{2}{2^2} + ... +\fra{2}{2^n})|)
La parenthèse de droite est inférieure à 1 donc, x étant un élément de I,
-f(\fra{x}{2^n})- x\,l (\fra{1}{2} + \fra{1}{2^2} + \fra{1}{2^3} + \fra{1}{2^4}+ ...+\fra{1}{2^n})|< \epsilon \, |x|)
Le membre de gauche est une suite
Comme f est continue en 0, sa limite quand n tend vers +infini est-f(0)- x\,l|)
cette limite est inférieure au second membre donc
-f(0)- x\,l| <\epsilon \, |x|)
-f(0)}{x}-l|<\epsilon)
f est donc dérivable en 0 et=l)
Par exemple, si on prend f(x)=sin x
-f(x)}{x}= \fra{2sin(x)cos(x)-sin(x)}{x}=\fra{sin(x)}{x}(2cos(x)-1))
la limite en 0 est bien 1 qui est le cosinus de 0
Je propose cette démonstration (à vérifier car pas trop sûr ...)
on pose
soit
la limite de m(x) quand x tend vers 0 étant 0.
soit n un entier fixé
D'après l'égalité 1, on a les égalités:
.....
.....
En additionnant membre à membre:
Comme la limite de m(x) quand x tend vers 0 est 0, soit un nombre
si x appartient à I=[-
on suppose donc que
Tous les
donc
La parenthèse de droite est inférieure à 1 donc, x étant un élément de I,
Le membre de gauche est une suite
Comme f est continue en 0, sa limite quand n tend vers +infini est
cette limite est inférieure au second membre donc
f est donc dérivable en 0 et
Par exemple, si on prend f(x)=sin x
la limite en 0 est bien 1 qui est le cosinus de 0
par Doraki » 31 Mai 2013, 10:19
Quitte à remplacer f(x) par f(x)-lx où l est la limite de (f(2x)-f(x))/x, on peut supposer l=0.
-f(0)}x| <br /> = \lim_{n \to \infty} |\frac{f(x)-f(x/2^n)}{x-x/2^n}|<br /> \le \lim_{n \to \infty} \sup_{x/2^n \le t \le x/2} |\frac{f(2t)-f(t)}t| <br /> = \sup_{0 < t \le x/2} |\frac{f(2t)-f(t)}t|)
.
Or comme ce dernier tend vers 0 quand x tend vers 0, lim (f(x)-f(0))/x existe et vaut 0.
(l'inégalité dit que la moyenne (pondérée) de trucs est plus petite que le plus gros de ces trucs)
Or comme ce dernier tend vers 0 quand x tend vers 0, lim (f(x)-f(0))/x existe et vaut 0.
(l'inégalité dit que la moyenne (pondérée) de trucs est plus petite que le plus gros de ces trucs)
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :