Simplification de sommes (trigo, complexes...)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yonyon
- Membre Naturel
- Messages: 42
- Enregistré le: 25 Mai 2005, 17:48
-
 par yonyon » 25 Aoû 2006, 22:55
par yonyon » 25 Aoû 2006, 22:55
Bonjour, je bloque pour cet exercice où il faut simplifier des sommes:
pour cette question, voilà ce que j'ai fait mais je ne suis pas très sûre de moi:

Pour les deux questions suivantes, je suis bloquée:
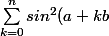})
à cause du carré, je ne vois pas comment simplifier...

Je ne vois pas du tout comment m'y prendre
Merci d'avance pour votre aide
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 26 Aoû 2006, 01:12
par nekros » 26 Aoû 2006, 01:12
Salut,
pour le premier exo, si n est pair, alors
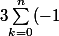^k C_n^k cos(ka+b)=2^n(-1)^{\frac{n}{2}} cos(b+\frac{an}{2})sin^n(\frac{a}{2}))
Tu as oublié la puissance n sur le sinus.
Sauf erreurs.
A+
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 26 Aoû 2006, 01:57
par nekros » 26 Aoû 2006, 01:57
Pour calculer
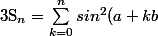)
, tu peux dériver
)
.
Reste à calculer
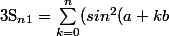)'=b \sum_{k=0}^n sin(2(a+kb)))
et tu en déduis
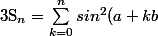)
.
Sauf erreurs.
A+
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 26 Aoû 2006, 02:01
par nekros » 26 Aoû 2006, 02:01
Pour la dernière, je trouve que
}{cos^k(a)}=\frac{sin(n+1)a}{sin(a)cos^n(a)})
si

n'est pas congru à
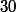
modulo
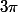
Je posterai le raisonnement demain, enfin tout à l'heure...
A+
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 26 Aoû 2006, 10:03
par nada-top » 26 Aoû 2006, 10:03
bonjour,
yonyon a écrit:Pour les deux questions suivantes, je suis bloquée:
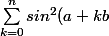})
à cause du carré, je ne vois pas comment simplifier...
si c'est le carré qui te gène peut-on pas utiliser ça :
)= 1- 2sin^2(a+kb))
donc
 = \frac{1-cos(2(a+kb))}{2})
en tous cas ce n'etait qu'une remarque en passant , je ne sais pas ou ça peut aller avec cette expression :ptdr:
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 26 Aoû 2006, 11:10
par Mikou » 26 Aoû 2006, 11:10
Ca tu l'aurai pas deja posté sur le forum bac a ... ? Si.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 26 Aoû 2006, 13:13
par nekros » 26 Aoû 2006, 13:13
Mikou a écrit:Ca tu l'aurai pas deja posté sur le forum bac a ... ? Si.
Salut Mikou,
De quoi tu parles ? :hein:
A+
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 26 Aoû 2006, 13:17
par Mikou » 26 Aoû 2006, 13:17
jdisai ca a yonyon qui apparement post sur plusieur forum a la foi le meme exo ..
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 26 Aoû 2006, 13:34
par alben » 26 Aoû 2006, 13:34
Mikou a écrit:Ca tu l'aurai pas deja posté sur le forum bac a ... ? Si.
Et aussi sur futura :we:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 26 Aoû 2006, 13:57
par nekros » 26 Aoû 2006, 13:57
Autre méthode pour la 1 :
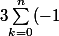^k C_n^k cos(\alpha k + \beta) = \sum_{k=0}^n (-1)^k C_n^k \frac{exp{i(\alpha k + \beta)}+exp{-i(\alpha k + \beta)}}{2}=\sum_{k=0}^n (-1)^k C_n^k \frac{(-exp{i \alpha})^k}{2} exp{i \beta}+\sum_{k=0}^n (-1)^k C_n^k \frac{(-exp{-i \alpha})^k}{2} exp{-i \beta}=\frac{exp{i \beta}}{2} (1-exp{i \alpha})^n+\frac{exp{-i \beta}}{2} (1-exp{-i \alpha})^n=Re((1-exp{i \alpha})^n exp{i \beta}))
Or,
^n=(exp{i \frac{\alpha}{2}}(exp{-i \frac{\alpha}{2}}-exp{i \frac{\alpha}{2}}))^n=exp{i n \frac{\alpha}{2}}(-2i sin(\frac{\alpha}{2}))^n)
Sauf erreurs.
A+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités


à cause du carré, je ne vois pas comment simplifier...