Exos suite numérique.

[eratos]

Salut les jeunes :happy2:

Alors, je suis sur un exercice là, et j'ai l'impression qu'il sert à rien.
Voilà l'énoncé:
La suite u(n) vérifie u(n+1)=f(un)
1) Donner la fonction numérique correspondante
2) Calculer les 4 1er termes de la suite

-----------Soit u(0)=1 et u(n+1)=-2(un)+3-----------

Donc:
1) La fonction numérique est f(x)=-2x+3
2) u(n)=-2u(n-1)+3
u(1)=-2u(0)+3= 1
u(2)=-2u(1)+3=1
u(3)=-2u(2)+3=1
u(4)=-2u(4)+3=1
La suite serait constante? Autrement, pourquoi me demande t'on de donner une fonction numérique, il y a bien une utilité? Je pige pas.

[Finrod]

1 est solution de f(x)=x... donc si ce sera toujours constant oui.

L'utilité dépend du niveau pour lequel est conçu l'exo.

L'étude de tous les cas de se fait en BAC+1.

ps : f et sont donnés dans l'énoncé ?

[eratos]

Niveau première...
Peut-être que de telles questions sont tout simplement pour l'entraînement :briques:

u0 est donné, mais pas f

[Finrod]

ah donc il faut essayer des f au hasard ?

Si c'est ça t'as juste pas eu de chance, c'est un cas particulier.

[Nightmare]

Salut,

concernant l'utilité de la question, c'est quand même bien de voir comment on génère les termes de la suite.

Ici, la suite est définie de manière récursive, c'est à dire qu'on donne son premier terme, puis au lieu de donner tous les autres par une formule génératrice, on se contente de donner le manière de passer d'un terme au suivant, et ce à l'aide d'une fonction numérique, qu'il est donc forcément utile de relever, puisque c'est elle qui permet de générer la suite. Du coup, l'étude de la fonction associée à la suite permet logiquement d'obtenir des informations sur la suite elle même, par exemple comme le signale Finrod, l'étude des points fixes de la fonction permet par exemple d'obtenir les éventuels candidats pour être limite de la suite, si elle converge. L'étude de la monotonie de f permet aussi de conclure quant à la monotonie de la suite, etc.

[eratos]

Ok, je commence à comprendre un peu comment ça marche.

Aujourd'hui, j'en suite à l'étude des sens de variations d'une suite.
Dans mon bouquin, il y a pas mal d'exercices mais seul les exos "type" sont corrigés, c'est pas plus mal, ça me force à réfléchir plus.

On me demande de calculer les premiers termes de la suite et d'étudier le sens de variations grâce au signe de .
a) Soit








Donc pour tout n de ,
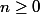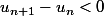
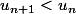. La suite est décroissante. J'ai bon?

[Nightmare]

Salut,

C'est presque bon, sauf que l'ordre est large est non stricte, comme le confirme le calcul des deux premiers termes, on a u0=u1.

[eratos]

Re.
Je viens d'acquérir une nouvelle technique ancestral pour trouver le sens de variation d'une suite numérique. Celle qui dit que si tout les termes de la suite sont strictement positif, alors on peut comparer le quotient de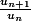 et 1.
La théorie ça va, mais pas la pratique.


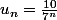
Ici, 7^n tend vers +infini quand n tend vers +infini et tend vers 0+.
On peut comparer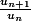 et 1


La suite est décroissante.
J'ai bon?

[Nightmare]

J'ai bon?

Tout à fait :happy3:

[xaroxhoandoxos]

quel est ton bouquin pliz pour ke je puisse mentrainer ossi cela na rien d'une reponse ki taidra me par contre moi si