Tangente à une courbe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
gg56
- Messages: 7
- Enregistré le: 24 Aoû 2006, 19:11
-
 par gg56 » 24 Aoû 2006, 19:26
par gg56 » 24 Aoû 2006, 19:26
Bonjour,
Je suis sur un problème et une question à laquelle je n'ai pas pu répondre.
J'ai une fonction f'x)=x^2 + 2x + 1
Il est demandé les équations des tangentes à la courbe C passant par l'origine du repère.
Je connais à l'aide de la dérivée, l'équation d'une tangente en un point de la courbe : y = (x-xo)f'(xo) + f(xo) mais je n'arrive pas à trouver l'equation demandée de la tangente à la courbe passant par l'origine .
Si qqun peut m'aider. Merci d'avance
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 24 Aoû 2006, 19:32
par nekros » 24 Aoû 2006, 19:32
Salut,
On a
=(x-a)f'(a)+f(a))
et
=2x+2)
On cherche l'équation de la tangente en
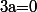
Or,
=2)
et
=1)
, donc l'équation de la tangente en
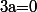
a est :

A+
-
gg56
- Messages: 7
- Enregistré le: 24 Aoû 2006, 19:11
-
 par gg56 » 24 Aoû 2006, 19:54
par gg56 » 24 Aoû 2006, 19:54
Merci de ta réponse,
Mais une chose m'intrigue.
La tangente à C doit passer par l'origine du repère. Or si l'équation est
y=2x + 1 alors pour x=0 ==> y=1 et cette tangente ne passe pas par l'origine.
Qu'en penses-tu ?
-
nimitz
- Membre Naturel
- Messages: 48
- Enregistré le: 09 Jan 2006, 19:22
-
 par nimitz » 24 Aoû 2006, 20:27
par nimitz » 24 Aoû 2006, 20:27
bonsoir,
f(x)=x²+2x+1
f'(x)=2x+2
y=f'(a)(x-a)+f(a)
or, lorsque x=0,
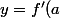 \times (-a)+f(a))
et
 \times (-a)+f(a)=0)
équivaut à a=1 ou a=-1
je te laisse finir.
sauf erreur.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 24 Aoû 2006, 20:34
par nekros » 24 Aoû 2006, 20:34
gg56 a écrit:Merci de ta réponse,
Mais une chose m'intrigue.
La tangente à C doit passer par l'origine du repère. Or si l'équation est
y=2x + 1 alors pour x=0 ==> y=1 et cette tangente ne passe pas par l'origine.
Qu'en penses-tu ?
Hum tu as raison, j'ai lu "tangente à l'origine de la courbe"
Dans ce cas, on trouve

qui passe bien par l'origine. Il suffit de résoudre

comme l'a dit
nimitz.
A+
-
gg56
- Messages: 7
- Enregistré le: 24 Aoû 2006, 19:11
-
 par gg56 » 24 Aoû 2006, 20:40
par gg56 » 24 Aoû 2006, 20:40
Salut
Merci Nimitz, c'est tout à fait juste
cela me donne 2 tangentes:
- La 1ère est l'axe ox cas ou a=-1
- La seconde cas ou a=1 est d'équation y=4x
A bentôt et bonne soirée
-
nimitz
- Membre Naturel
- Messages: 48
- Enregistré le: 09 Jan 2006, 19:22
-
 par nimitz » 24 Aoû 2006, 20:42
par nimitz » 24 Aoû 2006, 20:42
C'est bien ça :happy3:
bonne soirée.
-
gg56
- Messages: 7
- Enregistré le: 24 Aoû 2006, 19:11
-
 par gg56 » 24 Aoû 2006, 20:44
par gg56 » 24 Aoû 2006, 20:44
Ok Nekros , graphiquement ça marche.
Merci et à bientôt
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 24 Aoû 2006, 20:58
par Mikou » 24 Aoû 2006, 20:58
nimitz c'est un polytechncien tu crois quoi, bien joué frere.
-
nimitz
- Membre Naturel
- Messages: 48
- Enregistré le: 09 Jan 2006, 19:22
-
 par nimitz » 24 Aoû 2006, 21:01
par nimitz » 24 Aoû 2006, 21:01
:ptdr:
espérons que tu auras raison....mais j'en doute...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
