Probleme difficil avec la racines carrée

[etto]

bonjour tout le monde
quelqu'un peut m'aider svp

montrer que : racine(4a+1) + racine(4b+1) + racine(4c+1) =-1/4 et b>=-1/4 et c>=-1/4 et que a+b+c=1
merci d'avance

[Archibald]

Élève tes membres au carré pour faire disparaître le radical (la racine carrée)

[etto]

Élève tes membres au carré pour faire disparaître le radical (la racine carrée)

j'ai deja essayé mais sans resultat

[Archibald]

Et bien montre-nous à quoi tu es arrivé, en détaillant tes calculs.

[etto]

Et bien montre-nous à quoi tu es arrivé, en détaillant tes calculs.

la partie gauche au carre ca nous donne 23+2(ab+ac+bc)

[Archibald]

Ça, ça m'étonnerait

[Black Jack]

Ça, ça m'étonnerait

C'est une boutade ou c'est sérieux ?

:zen:

[etto]

j'ai utilisé la formule (a+b+c)²=a²+b²+c²

[Archibald]

+2ab+2bc+2ac *

[etto]

+2ab+2bc+2ac *

oui c ca ce que j'ai fais

[etto]

bonsoir tout le monde
personne n'a trouvé une solution à mon problème

[Robic]

Je découvre ce problème très intéressant ! (Je venais ici de temps en temps sans être connecté, ce problème m'a donné l'occasion de m'inscrire.)

J'ai réussi à le résoudre en utilisant uniquement les outils du lycée, mais c'est vrai qu'il n'était pas évident. Ce qui le rend difficile, c'est que l'inégalité est assez fine (mais on peut faire mieux !), elle ne s'obtient pas trivialement en minorant chaque racine carrée (qu'on mette tout au carré comme proposé au début de cette discussion n'y change rien).

Je vais détailler la première méthode, celle qui ne marche pas, puis donner l'idée de la deuxième (celle qui marche) sans détailler puisque ce n'est pas le but de ce forum.

Première méthode :

Les trois premières conditions expriment simplement que les racines carrées sont définies, c'est la quatrième condition qui fait marcher le truc : .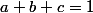

Ainsi, on a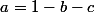 . Comme b et c sont supérieurs ou égaux à -1/4 on en déduit que . Ceci permet de majorer par 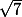. Bien sûr, ceci reste vrai pour la racine carrée en b et celle en c, de sorte que leur somme est majorée par 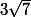. Hélas, ce nombre est plus grand que 5, ça ne démontre pas le résultat demandé.

Le problème, c'est que lorsqu'une des racines carrées atteint son maximum (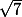), on voit bien que les deux autres sont forcément plus petites. En effet, la condition 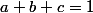fait que lorsqu'un des trois nombres est grand, un des deux autres est petit. Quand l'un atteint son maximum, les deux autres atteignent leur minimum. Majorer brutalement chaque racine carrée par son maximum possible était trop brutal.

Solution : considérer cette expression comme une fonction de deux variables (pas de trois puisque l'une des trois s'écrit en fonction des deux autres) et étudier ses variations. Comme les fonctions de deux variables ne sont pas au programme du lycée, j'ai défini une fonction d'une seule variable dépendant d'un paramètre qui est la deuxième.

Deuxième méthode :

On voit bien que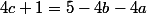 , du coup on va étudier la fonction définie par : pour a et b dans (c'est bien l'expression qu'on cherche à majorer).

Plan :
1) Étudier les variations de et montrer qu'elle admet un maximum. Exprimer ce maximum en fonction de b.
2) On pose M(b) = maximum de la fonction (il dépend de b). Étudier les variations de la fonction M et montrer qu'elle atteint un maximum en b=1/3 (que valent alors a et c ?) qui vaut . Ce qui résout le problème (en mieux !).

[Carpate]

Je découvre ce problème très intéressant ! (Je venais ici de temps en temps sans être connecté, ce problème m'a donné l'occasion de m'inscrire.)

J'ai réussi à le résoudre en utilisant uniquement les outils du lycée, mais c'est vrai qu'il n'était pas évident. Ce qui le rend difficile, c'est que l'inégalité est assez fine (mais on peut faire mieux !), elle ne s'obtient pas trivialement en minorant chaque racine carrée (qu'on mette tout au carré comme proposé au début de cette discussion n'y change rien).

Je vais détailler la première méthode, celle qui ne marche pas, puis donner l'idée de la deuxième (celle qui marche) sans détailler puisque ce n'est pas le but de ce forum.

Première méthode :

Les trois premières conditions expriment simplement que les racines carrées sont définies, c'est la quatrième condition qui fait marcher le truc : .

Ainsi, on a . Comme b et c sont supérieurs ou égaux à -1/4 on en déduit que . Ceci permet de majorer par . Bien sûr, ceci reste vrai pour la racine carrée en b et celle en c, de sorte que leur somme est majorée par . Hélas, ce nombre est plus grand que 5, ça ne démontre pas le résultat demandé.

Le problème, c'est que lorsqu'une des racines carrées atteint son maximum (), on voit bien que les deux autres sont forcément plus petites. En effet, la condition fait que lorsqu'un des trois nombres est grand, un des deux autres est petit. Quand l'un atteint son maximum, les deux autres atteignent leur minimum. Majorer brutalement chaque racine carrée par son maximum possible était trop brutal.

Solution : considérer cette expression comme une fonction de deux variables (pas de trois puisque l'une des trois s'écrit en fonction des deux autres) et étudier ses variations. Comme les fonctions de deux variables ne sont pas au programme du lycée, j'ai défini une fonction d'une seule variable dépendant d'un paramètre qui est la deuxième.

Deuxième méthode :

On voit bien que , du coup on va étudier la fonction définie par : pour a et b dans (c'est bien l'expression qu'on cherche à majorer).

Plan :
1) Étudier les variations de et montrer qu'elle admet un maximum. Exprimer ce maximum en fonction de b.
2) On pose M(b) = maximum de la fonction (il dépend de b). Étudier les variations de la fonction M et montrer qu'elle atteint un maximum en b=1/3 (que valent alors a et c ?) qui vaut . Ce qui résout le problème (en mieux !).

Solution un peu tardive
On facilite l'écriture en posant :
: , ,

En sommant terme à terme les 3 inégalités:

[Robic]

Ah oui, c'est quand même plus simple que ce que j'avais fait !

(Par contre ça ne prouve pas que est le meilleur majorant possible...)

[Carpate]

Ah oui, c'est quand même plus simple que ce que j'avais fait !

(Par contre ça ne prouve pas que est le meilleur majorant possible...)

Oui, c'est vrai mais l'énoncé ne le demandait pas ...

[Carpate]

Ah oui, c'est quand même plus simple que ce que j'avais fait !

(Par contre ça ne prouve pas que est le meilleur majorant possible...)

On le prouve en faisant appel à la géométrie
Avec les notations de mon message précédent :
Soient et 2 points de l'espace euclidien de repère orthonormal

: décrit le quart de sphère S de centre et de rayon , surface dont les limites sont les intersections de la sphère avec les plans

Lorsque O,A,M sont alignés (le point M est alors à l'intersection de [0A) et de S), le produit scalaire est maximal et vaut et cette position est unique.
Lorsque M se trouve sur l'une des limites de S,
Lorsque M décrit S, décrit et l'on a l'encadrement :

[Robic]

Ah c'est pas bête d'avoir mis de la géométrie dans les calculs ! J'aime beaucoup cette démonstration. Elle donne le majorant, prouve que c'est le meilleur, qu'il est unique, et donne même un minorant !

(Cela dit je ne suis pas convaincu que l'angle maximum possible soit . En particulier il n'est pas obtenu sur les limites de S (ni sur les axes, ni sur les plans) mais plutôt quand M est à l'intersection de la sphère et de la droite dirigée par i+j ou bien sur le pôle nord de la sphère. Si M est sur l'axe des x, par exemple, ça donne 54° et quelques. Ce ne serait pas lui l'angle maximal ?)

[Carpate]

Ah c'est pas bête d'avoir mis de la géométrie dans les calculs ! J'aime beaucoup cette démonstration. Elle donne le majorant, prouve que c'est le meilleur, qu'il est unique, et donne même un minorant !

(Cela dit je ne suis pas convaincu que l'angle maximum possible soit . En particulier il n'est pas obtenu sur les limites de S (ni sur les axes, ni sur les plans) mais plutôt quand M est à l'intersection de la sphère et de la droite dirigée par i+j ou bien sur le pôle nord de la sphère. Si M est sur l'axe des x, par exemple, ça donne 54° et quelques. Ce ne serait pas lui l'angle maximal ?)

Tu as raison
D'abord, je me suis trompé dans l'évaluation de l'angle que fait OA avec chacun des plans xoy, xoz, yoz (et qui n'est donc pas l'angle maximum).
Sa tangente vaut soit de l'ordre de 35° (OA est une "diagonale" du cube construit sur )
Quant à l'angle maximum, quand M est sur un des trois axes du repère, ici M sur :

soit un angle ~ 54°
L'encadrement serait donc :

[Robic]

Voilà, c'est ce que j'avais trouvé. En tout cas cette méthode est excellente !

[chan79]

Tu as raison
D'abord, je me suis trompé dans l'évaluation de l'angle que fait OA avec chacun des plans xoy, xoz, yoz (et qui n'est donc pas l'angle maximum).
Sa tangente vaut soit de l'ordre de 35° (OA est une "diagonale" du cube construit sur )
Quant à l'angle maximum, quand M est sur un des trois axes du repère, ici M sur :

soit un angle ~ 54°
L'encadrement serait donc :

Bravo pour l'interprétation géométrique.
Pour la minoration, il y avait aussi:

donc