Dérivabilité d'une fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
George150
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Déc 2012, 20:36
-
 par George150 » 28 Avr 2013, 21:53
par George150 » 28 Avr 2013, 21:53
Bonjour je vais bientôt passer un concours et je voudrais connaître une méthode pour savoir si une fonction est dérivable en 0 ou non.
Par exemple comment savoir si f(x) = x|x| est dérivable en 0
-
ledoyen
- Membre Naturel
- Messages: 85
- Enregistré le: 23 Avr 2009, 15:45
-
 par ledoyen » 28 Avr 2013, 22:47
par ledoyen » 28 Avr 2013, 22:47
Voici la réponse
[url]http://fr.wikipedia.org/wiki/Dérivabilité[/url]
-
George150
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Déc 2012, 20:36
-
 par George150 » 28 Avr 2013, 23:02
par George150 » 28 Avr 2013, 23:02
Merci de ton aide donc pour mon exemple j'ai utilisé la 1ère formule et je tombe sur

= 0 c'est bien ça ?
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 29 Avr 2013, 00:24
par Archibald » 29 Avr 2013, 00:24
= \lim_{h \to 0} \frac{f(0+h)-f(0)}{h} = <br /> \lim_{h \to 0} \frac{(0+h)|0+h| - 0|0|}{h} = \lim_{h \to 0} \frac{h|h|}{h} = \lim_{h \to 0} |h|)
Qu'en conclues-tu ?
-
George150
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Déc 2012, 20:36
-
 par George150 » 29 Avr 2013, 11:12
par George150 » 29 Avr 2013, 11:12
Archibald a écrit:= \lim_{h \to 0} \frac{f(0+h)-f(0)}{h} = <br /> \lim_{h \to 0} \frac{(0+h)|0+h| - 0|0|}{h} = \lim_{h \to 0} \frac{h|h|}{h} = \lim_{h \to 0} |h|)
Qu'en conclues-tu ?
J'en conclus que

tend vers 0 et donc que la fonction est bien dérivable en 0 c'est bien ça non ?
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 29 Avr 2013, 18:30
par Archibald » 29 Avr 2013, 18:30
Pas très rigoureuse comme conclusion...
-
George150
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Déc 2012, 20:36
-
 par George150 » 29 Avr 2013, 19:55
par George150 » 29 Avr 2013, 19:55
Archibald a écrit:Pas très rigoureuse comme conclusion...
Je vois pas vraiment comme l'améliorer, mais mon concours se base seulement sur des QCM donc je pense pas que ça m'aidera si je conclu ou non. Sinon pourrais-tu m'aider pour celui là ? Je n'arrive pas vraiment à le résoudre
 = x^{2}+2\\<br />f(x) = x^{3}-x{2}+2<br />\end{array}<br />\right.)
Pour la 1ère équation c'est si
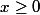
Pour la 2ème c'est si x < 0
Je me retrouve avec la 1ère équation une limite vers plus +

en utilisant la 1ère méthode de wikipédia, donc la fonction n'est pas définie en 0 pour cette fonction. Or dans l'annale il y a écrit que la fonction est bien définie sur 0. Peux-tu m'expliquer pourquoi ?
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 29 Avr 2013, 21:31
par Archibald » 29 Avr 2013, 21:31
Ce sont pourtant de simples fonctions polynomiales, elles sont continues et dérivables sur

.
Je peux savoir quelle formule as-tu utilisée, et surtout qu'est-ce que tu en as compris ?
-
George150
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Déc 2012, 20:36
-
 par George150 » 30 Avr 2013, 00:13
par George150 » 30 Avr 2013, 00:13
Archibald a écrit:Ce sont pourtant de simples fonctions polynomiales, elles sont continues et dérivables sur

.
Je peux savoir quelle formule as-tu utilisée, et surtout qu'est-ce que tu en as compris ?
J'ai utilisé la 1ère formule :
-f(a)}{x-a})
. De ce que j'ai compris c'est que si une j'utilise cette formule et que je tombes sur un nombre fini, j'en conclut que la fonction est dérivable en ce point. J'ai peut-être des lacunes dessus vu qu'on a pas vraiment étudier ces questions en classe ou bien très rapidement, on a surtout dérivée les fonctions
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 30 Avr 2013, 02:53
par Carpate » 30 Avr 2013, 02:53
George150 a écrit:J'ai utilisé la 1ère formule :
-f(a)}{x-a})
. De ce que j'ai compris c'est que si une j'utilise cette formule et que je tombes sur un nombre fini, j'en conclut que la fonction est dérivable en ce point. J'ai peut-être des lacunes dessus vu qu'on a pas vraiment étudier ces questions en classe ou bien très rapidement, on a surtout dérivée les fonctions
Si c'est un QCM, on ne te demande pas une démonstration directe de la dérivabilité de
 = x^2+2)
Sinon,
=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h})
-f(x)}{h}=\frac{(x+h)^2+2-(x^2+2)}{h}=\frac{h^2+2hx}{h}=2x+h)
=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}=2x)
-
George150
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Déc 2012, 20:36
-
 par George150 » 01 Mai 2013, 13:08
par George150 » 01 Mai 2013, 13:08
Okey merci beaucoup de votre aide :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
.
. De ce que j'ai compris c'est que si une j'utilise cette formule et que je tombes sur un nombre fini, j'en conclut que la fonction est dérivable en ce point. J'ai peut-être des lacunes dessus vu qu'on a pas vraiment étudier ces questions en classe ou bien très rapidement, on a surtout dérivée les fonctions
