Majoration et matrices.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 27 Avr 2013, 08:59
par Kikoo <3 Bieber » 27 Avr 2013, 08:59
Bonjour,
Je bloque sur une petite inégalité à établir.
Soit
, \exists (m,m',M,M')\in R^4 / m\leq f\leq M,\,m'\leq f^{(2)}\leq M'\})
J'ai montré que pour n=2 et

, nous avons :
\, :\,\forall (x,h)\in\mathbb{R}^2\, |f(x+h)-f(x)-hf'(x)|\leq \frac{\mathcal{M}_2h^2}{2})
avec
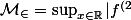}(x)|)
(et en général,
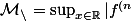}(x)|)
) grâce à Taylor-Lagrange.
Maintenant, on me demande d'appliquer (1) avec h=t puis h=-t (t>0) afin de montrer que :
|\leq \frac{\mathcal{M}_2t}{2}+ \frac{\mathcal{M}_0}{t})
mais je ne vois pas vraiment comment faire pour y arriver...
J'ai essayé comme pour une autre inégalité (
|\leq \frac{\mathcal{M}_2h}{2}+ \frac{2\mathcal{M}_0}{h})
) de découper ma valeur absolue en deux morceaux via la seconde inégalité triangulaire puis utiliser à nouveau l'ingalité triangulaire pour majorer f(x+h) et f(x) par leur sup.
Mais dans ce cas-ci, je bloque.
Merci !
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 27 Avr 2013, 10:54
par jlb » 27 Avr 2013, 10:54
salut, tu ecris les expressions pour t et -t
puis avec inégalité triangulaire et tes expressions tu majores |f(x+t) + f(x-t) - 2 f(x)|
encore un coup d'inégalité triangulaire pour majorer |f(x+t)-f(x-t)|, une fois là tu divises tout par 2t et tu fais tendre t vers 0 en écrivant |f(x+t)+f(x-t)|=|f(x+t)-f(x)+(f(x-t)-f(x))|
bon courage
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 27 Avr 2013, 11:17
par jlb » 27 Avr 2013, 11:17
tu écris les 2 expressions demandées, tu les ajoutes
tu utilises ensuite |a-b|=<|a|+|b|, tu simplifies le "a-b" et tu utilises enfin |u|-|v|=<|u-v|, cela doit te permettre d'isoler 2tf'(x) et en divisant par 2t tu obtiens l'inégalité apèrs avoir majoré |f(x-t)-f(x+t)| par 2 Mo.
à vérifier!!, bon courage
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 27 Avr 2013, 11:53
par Kikoo <3 Bieber » 27 Avr 2013, 11:53
Merci bien, jlb ;) Je vais tester de suite.
Edit : Ca fonctionne bien. Super !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 28 Avr 2013, 20:12
par Kikoo <3 Bieber » 28 Avr 2013, 20:12
Soit la matrice
!}\\<br />\frac{h_2}{1!} & \frac{h_{2}^{2}}{2!} & \cdots & \frac{h_2^{n-1}}{(n-1)!}\\<br />\vdots & \vdots & \ddots & \vdots\\<br />\frac{h_{n-1}}{1!} & \frac{h_{n-1}^2}{2!} & \cdots & \frac{h_{n-1}^{n-1}}{(n-1)!}\\<br />\end{bmatrix})
de
)
.
Il me faut résoudre
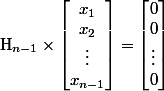
.
J'ai donc à résoudre le système que voici :
!}x_{n-1}=0 \\<br />\frac{h_2}{1!}x_1+\frac{h_{2}^{2}}{2!}x_2+\cdots + \frac{h_2^{n-1}}{(n-1)!}x_{n-1}=0 \\<br />\vdots \\<br />\frac{h_{n-1}}{1!}x_1+\frac{h_{n-1}^{2}}{2!}x_2+\cdots + \frac{h_{n-1}^{n-1}}{(n-1)!}x_{n-1}=0\\<br />\end{cases})
Et on me propose de considérer
=x_1+t \frac{x_2}{2!}+\cdots + \frac{x_{n-1}}{(n-1)!}t^{n-2})
.
Or je vois bien que les degrés sont décalés par rapport aux indices, mais je n'ai vraiment aucune idée de ce qu'il faut faire !
Merci de m'aiguiller un peu

-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 29 Avr 2013, 07:52
par jlb » 29 Avr 2013, 07:52
salut,
considère la fonction polynome t-->t*p(t) c'est de degré n-1 et combien a-t-elle de racines si x1,x2,...,xn-1 sont solutions du système dans le cas où les hi sont différents et différents de 0( rem: cela se voit et tu as une alternative plus classe car Hn-1 est presque une matrice de Vandermonde (multiplie la 1ere colonne par 1!, la 2eme par 2! la 3eme par 3!...cela te donne que le système est de Cramer (en calculant le déterminant de ce Vandermonde) donc inversible donc solution (0,0,...,0) quand les hi sont différents et non nuls)
Par contre si des hi sont identiques je ne vois pas trop??? Mais bon dans ton pb, c'est peut-être une hypothèse? car sinon, on enlève des lignes et il y aura des solutions pour la même raison en fonction d'indéterminées et cela doit se compliquer. si quelqu'un a une idée?
dans tous les cas, bon courage.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Avr 2013, 10:02
par Kikoo <3 Bieber » 29 Avr 2013, 10:02
Salut jlb ! :)
J'avais oublié de préciser que les hi (i de 1 à n-1) sont bel et bien tous distincts, et effectivement si on multiplie chaque ligne par les k!, on obtient une matrice de Vandermonde à coefficients distincts ligne par ligne, et donc inversible (c'est le but de la question d'après ^^).
Par contre, je n'ai pas encore été sur le chapitre "déterminants", donc Cramer je l'ai juste vu pour des 2*2 ou des 3*3 en début d'année, c'est tout. M'enfin je suis pas censé utiliser un calcul de déterminant.
Je vais essayer de chercher quelque chose, merci encore !
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 29 Avr 2013, 10:54
par jlb » 29 Avr 2013, 10:54
Kikoo <3 Bieber a écrit:Salut jlb !

J'avais oublié de préciser que les hi (i de 1 à n-1) sont bel et bien tous distincts, et effectivement si on multiplie chaque ligne par les k!, on obtient une matrice de Vandermonde à coefficients distincts ligne par ligne, et donc inversible (c'est le but de la question d'après ^^).
Par contre, je n'ai pas encore été sur le chapitre "déterminants", donc Cramer je l'ai juste vu pour des 2*2 ou des 3*3 en début d'année, c'est tout. M'enfin je suis pas censé utiliser un calcul de déterminant.
Je vais essayer de chercher quelque chose, merci encore !
relis alors le début de mon post!!! t*P(t) est de degré n-1 et à n racines ( 0 et les hi si x1,..xn-1 solution) ces coeff sont donc nuls!!cela te donne la solution (0,0,0....) (si les hi sont en plus diff de 0 cela doit être le cas aussi, non?)
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Avr 2013, 11:01
par Kikoo <3 Bieber » 29 Avr 2013, 11:01
jlb a écrit:relis alors le début de mon post!!! t*P(t) est de degré n-1 et à n racines ( 0 et les hi si x1,..xn-1 solution) ces coeff sont donc nuls!!cela te donne la solution (0,0,0....) (si les hi sont en plus diff de 0 cela doit être le cas aussi, non?)
Ok, mais la raison pour laquelle je bloquais tout à l'heure, c'est parce que je ne comprenais pas pourquoi un polynôme de degré n-1 pouvait avoir n racines distinctes. Je m'étais donc embrouillé pour rien car il s'agissait de l'issue du problème !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
