Probabilités

[Mitch51]

Bonjour à tous,

voici l'énoncé du problème qui me pose quelques soucis...Je vous remercie par avance de me donner quelques pistes de réflexion pour la réponse?

Bien cordialement,

Mitch


Les compagnies ferroviaires considèrent que 9 clients sur 10 ayant acheté un billet se présentent effectivement le jour même pour prendre ce train.

Combien de place une compagnie doit-elle proposer à la réservation pour que son train Paris-Marseille de 117 places ait 9 chances sur 10 d'être plein?

[leon1789]

être plein?

être plein, pour un train de 117 places, c'est -A- ou -B- ?

-A- avoir "au moins" 117 voyageurs sur le quai (et donc certains vont rester sans place assise : les joies de la surréservation...)

-B- avoir "exactement" 117 voyageurs sur le quai (et tout le monde aura pile-poil une et une seule place assise)

[Mitch51]

être plein, pour un train de 117 places, c'est -A- ou -B- ?

-A- avoir "au moins" 117 voyageurs sur le quai (et donc certains vont rester sans place assise : les joies de la surréservation...)

-B- avoir "exactement" 117 voyageurs sur le quai (et tout le monde aura pile-poil une et une seule place assise)

je pense à -A- en effet, c'est ce qui se rapproche le plus de la réalité...Et vous?

[hammana]

Bonjour à tous,

voici l'énoncé du problème qui me pose quelques soucis...Je vous remercie par avance de me donner quelques pistes de réflexion pour la réponse?

Bien cordialement,

Mitch


Les compagnies ferroviaires considèrent que 9 clients sur 10 ayant acheté un billet se présentent effectivement le jour même pour prendre ce train.

A mon avis l'énoncé du problème n'a pas de sens. Combien de personnes se présenteront si 50 personnes ont acheté un billet?

[Mitch51]

A mon avis l'énoncé du problème n'a pas de sens. Combien de personnes se présenteront si 50 personnes ont acheté un billet?

9 personnes sur 10, donc 45 personnes

[Mitch51]

C'est cette partie qui me turlupine :

"Combien de place une compagnie doit-elle proposer à la réservation pour que son train Paris-Marseille de 117 places ait 9 chances sur 10 d'être plein?"



Pour qu'il ait 100% de chance d'être plein, partant du postulat que 9 personnes sur 10 se présentent effectivement le jour du départ :
x étant le nombre de réservations :

(9/10)x=117
donc x=117(10/9)
x=130

Pour 100% de chances de remplissage du train, il faut donc au moins 130 réservations.

Mais pour 9 chance sur 10 de 100% de remplissage...Je ne suis pas très inspiré :mur:

[hammana]

9 personnes sur 10, donc 45 personnes

qu'arriverait-il si le nombre de personnes n'était pas un multiple de 10 (45 par exemple)

[leon1789]

hammana, c'est un exo de proba, il a bien du sens... Tes questions ne sont pas les bonnes, ce n'est pas comme ça qu'il faut aborder cet exo !

je pense à -A- en effet, c'est ce qui se rapproche le plus de la réalité...Et vous?

Je suis du même avis, sinon l'exo n'est pas faisable je crois. On part sur ça.

Je résume la donnée de l'exercice :
quand une personne a acheté un billet, la probabilité qu'elle soit présente le jour J heure H est p = 9/10 . OK ?
Ca, c'est une loi de Bernoulli de paramètre p (la personne est là avec une proba de p, ou bien elle n'est pas là avec une proba de 1-p)


Maintenant, si la société du train vend n billets, quelle est la probabilité que exactement k personnes soient présentes ? (indice : où suit une loi de Bernoulli de paramètre p)

Seconde question : si la société du train vend n billets, quelle est la probabilité qu' au moins k personnes soient présentes ? ( indice )

[hammana]

hammana, c'est un exo de proba, il a bien du sens... Tes questions ne sont pas les bonnes, ce n'est pas comme ça qu'il faut aborder cet exo !



Je suis du même avis, sinon l'exo n'est pas faisable je crois. On part sur ça.

Je résume la donnée de l'exercice :
quand une personne a acheté un billet, la probabilité qu'elle soit présente le jour J heure H est p = 9/10 . OK ?
Ca, c'est une loi de Bernoulli de paramètre p (la personne est là avec une proba de p, ou bien elle n'est pas là avec une proba de 1-p)


Maintenant, si la société du train vend n billets, quelle est la probabilité que exactement k personnes soient présentes ? (indice : où suit une loi de Bernoulli de paramètre p)

Seconde question : si la société du train vend n billets, quelle est la probabilité qu' au moins k personnes soient présentes ? ( indice )

Un énoncé réaliste serait de dire par exemple que d'après les statistiques de la SNCF, la moyenne des personnes qui se présentent est de 90%, qu'elle suit la loi normale, et donner son écart type. L'énoncé tel que présenté donne une certitude, il n'est plus question de probabilité, mais d'une simple règle de trois.

[leon1789]

Un énoncé réaliste serait de dire par exemple que d'après les statistiques de la SNCF, la moyenne des personnes qui se présentent est de 90%, qu'elle suit la loi normale, et donner son écart type. L'énoncé tel que présenté donne une certitude, il n'est plus question de probabilité, mais d'une simple règle de trois.

ah tiens, la loi normale :ptdr: ça faisait longtemps !

Parler de la loi normale (hors programme de 1ère) incite naturellement les élèves à utiliser la loi normale pour répondre à l'exo. Or, il me semble que l'exo est en lien avec la loi binomiale (on travaille sur des entiers, entre 0 et 200).

Mais non, pas de règle de trois : "9 personnes sur 10" sous-entend "en moyenne" et signifie évidemment que la proba d'être présent est p = 0.9 (ok, l'énoncé aurait pu être mieux écrit de ce coté là). De plus, en supposant que les présences des clients sont indépendantes, il s'ensuit une loi de probabilité binomiale. On pourra calculer le nombre n minimum de billets à vendre pour "être sûr à 90%" (bien préciser ce que cela signifie) qu'au moins 117 passagers seront présents au départ.

Enfin, si tu veux, on pourra alors approximer la loi binomiale par une loi normale de moyenne np et de variance np(1-p) (inutile que l'énoncé précise l'écart-type, on peut le retrouver).

[leon1789]

Je résume la donnée de l'exercice :
quand une personne a acheté un billet, la probabilité qu'elle soit présente le jour J heure H est p = 9/10 . OK ?
Ca, c'est une loi de Bernoulli de paramètre p (la personne est là avec une proba de p, ou bien elle n'est pas là avec une proba de 1-p)


Maintenant, si la société du train vend n billets, quelle est la probabilité que exactement k personnes soient présentes ? (indice : où suit une loi de Bernoulli de paramètre p)

ha, je n'aurais pas dû présenter la somme des variables , mais dire simplement qu'on répétait n fois la même expérience de Bernoulli, ce qui donne une loi ........

En effet, je crois bien qu'au lycée on ne parle pas de somme de variables aléatoires. :triste:

[Mitch51]

ha, je n'aurais pas dû présenter la somme des variables , mais dire simplement qu'on répétait n fois la même expérience de Bernoulli, ce qui donne une loi ........

En effet, je crois bien qu'au lycée on ne parle pas de somme de variables aléatoires. :triste:

Oui je pense bien qu'il s'agit d'une loi binomiale, merci beaucoup!

En revanche j'ai aussi une difficulté sur le nombre de répétitions de l'expérience. Mais je vais jusqu'au bout de mon raisonnement pour vous montrer :

Partons du principe qu'on souhaite exactement 117 passagers,

je pense qu'il faut répéter n fois l'expérience, à savoir 117+A (notre nombre de réservations) ou A est notre inconnue.

Du coup notre loi binomiale devient :

P(X=117) = 0,9 (90% de chance pour le train d'être plein avec 117 passagers)
(117 parmi 117+A)*(p^117)*(117+A -117) = 0,9

avec p la probabilité qu'un passage se présente effectivement : p=0,9

(117 parmi 117+A)*(0,9^117)*(A) = 0,9

et on obtient la réponse, en extrayant A et en donnant le nombre de réservations recherché : 117+A

Encore merci pour votre aide. Que pensez-vous de ce raisonnement?

Mitch

[leon1789]

je pense qu'il faut répéter n fois l'expérience, à savoir 117+A (notre nombre de réservations) ou A est notre inconnue.

jusqu'ici, c'est ok. Mais après ça ne va plus.

Du coup notre loi binomiale devient :

P(X=117) = 0,9 (90% de chance pour le train d'être plein avec 117 passagers)

Poser P(X=117) = 0.9, c'est vouloir résoudre la version -B- du problème (voir mon premier message).
On s'est mis d'accord pour résoudre la version -A-. Donc il faut résoudre .

(117 parmi 117+A)*(p^117)*(117+A -117) = 0,9

heu, il manque (1-p).

La loi binomiale B(n,p), c'est P(X=k) = (k parmi n) . p^k . (1-p)^(n-k)
ce qui donne ici P(X=k) = (k parmi 117+A) . p^k . (1-p)^(117+A-k)

Ne pas poser k=117 tout de suite, car on aura besoin de plus tard !

avec p la probabilité qu'un passage se présente effectivement : p=0,9

ce qui donne ici P(X=k) = (k parmi 117+A) . 0,9^k . 0,1^(117+A-k)

Maintenant que vaut ?

[Mitch51]

jusqu'ici, c'est ok. Mais après ça ne va plus.


Poser P(X=117) = 0.9, c'est vouloir résoudre la version -B- du problème (voir mon premier message).
On s'est mis d'accord pour résoudre la version -A-. Donc il faut résoudre .


heu, il manque (1-p).

La loi binomiale B(n,p), c'est P(X=k) = (k parmi n) . p^k . (1-p)^(n-k)
ce qui donne ici P(X=k) = (k parmi 117+A) . p^k . (1-p)^(117+A-k)

Ne pas poser k=117 tout de suite, car on aura besoin de plus tard !


ce qui donne ici P(X=k) = (k parmi 117+A) . 0,9^k . 0,1^(117+A-k)

Maintenant que vaut ?

Je dirais 1-P(X<117)....

mais perplexe quant à A et k, mon état de fatigue sûrement mais on se retrouve avec deux inconnues?

[leon1789]

Je dirais 1-P(X<117)....

c'est vrai, mais ce n'est pas ça qui va faire le calcul :lol3:
est la proba d'avoir , autrement 117 ou 118 ou...
Tu peux le formaliser = ... avec une somme ?

[lecar]

Bonjour,

Il s'agit effctivement d'une loi binomiale (à rédiger correctement) à savoir:

quelle est l'épreuve de Bernouilli répétée?
issues possibles et probabilités associées?
Indépendance des épreuves de Bernouilli répétées
quelle est la variable aléatoire associée (dépend de ce que l'on a choisi pour les issues au départ...)

Ici, ça donne:

On considère l'épreuve de Bernouilli consisatnt à choisir un voyageur au hasard ayant acheté un billet avec les issues S: "il se présente" et E=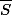 :" il ne se présente pas" avec les probabilités.......
...

....

la variable aléatoire X donnant le nombre de voyageurs ayant acheté un billet se présentant suit une loi.........de paramètres.....


Ensuite, on veut donc pour que le train soit plein mais pas plus que 117 voyageurs exactement se présentent avec la probabilité 0,9

Là en première, c'est avec la calculatrice qu'il faut opérer (notamment MENU STAT puis DIST puis BINM puis Bpd pour les casio)

Chercher ensuite n pour que p(X=117)=0,9 environ.....

Sur ce lien, une peu d'aide sur la rédaction et l'utilisation de la calculatrice pour la loi binomiale:


Méthode loi binomiale

calculs avec casio

ou avec TI méthode TI

Cordialement,

J-F L ( maths-s.fr )

[leon1789]

Chercher ensuite n pour que p(X=117)=0,9 environ.....

Ah, je demande à voir votre solution à cette équation !
Pour une loi binomiale avec des paramètres comme ici, c'est évidemment impossible d'avoir la proba d'un seul événement (X=117) aussi élevée : environ 90% (ou davantage) . :mur: Un tel soutien scolaire (maths-s.fr), c'est raté . :marteau:

Pour info, la proba de cet événement (X=117) ne dépassera jamais 10% , quel que soit n ! :hum:

C'est bien qu'il faut résoudre en l'inconnue n.

[lecar]

Bonjour,

Pour éviter de polémiquer inutilement plus longtemps mais pour répondre tout de même à l'ironie de l'interlocuteur précédent......

Effectivement, il n'y a aucune possibilité pour p(X=117)=0,9, il suffit de faire quelques tests à la calculatrice pour s'en apercevoir mais un élève de première S n'a pas d'autre solution pour s'en sortir que de chercher la valeur max en tatonant....

ou bien en ayant une idée plutôt précise (ce qui est plutôt rare vu le programme) de ce qui se passe au niveau de la représentation graphique lorsque l'on joue sur le paramètre n, on peut utiliser GEOGEBRA pour se fixer une idée en créant un curseur pour n:

lien sur l'image geogebra

Si on cherche , on écrit alors



Ensuite avec la calculatrice (MENU STAT puis DIST puis BINM puis Bcd pour la casio), on obtient en saisissant X=116 puis n=135 puis p=0,9

et en saisissant X=116 puis n=134 puis p=0,9

calculatrice calculatrice

Encore faut-il savoir ce qu'il y a dans le programme de première S.....

Je ne sais quel était le but de l'ex, se servir de GEOGEBRA (sol 1) ou bien de la calculatrice (sol 2)

quand à écrire une équation avec inconnue n, pour info comme il l'a été dit précédemment on est bien loin de ce que l'on demande en première S....

et pour finir: "Bien juger, c'est juger avec raison et connaissance"...

"" La première des vertus est la prudence. ".....

Cordialement

J-F L

[leon1789]

Effectivement, il n'y a aucune possibilité pour p(X=117)=0,9, il suffit de faire quelques tests à la calculatrice pour s'en apercevoir mais un élève de première S n'a pas d'autre solution pour s'en sortir que de chercher la valeur max en tatonant....

> :hein:
S'il faut une calculatrice pour s'apercevoir que cette phrase a de très fortes chances d'être fausse, c'est que, à mon avis, l'élève manque sérieusement d'intuition et de bon sens (voir le 3ème message de cette discussion où Mitch51 comprend très bien que ce ne peut être ça).

Là encore, l'égalité n'a aucune chance d'être vérifiée car nous sommes en terrain discret.
C'est pour cela qu'il vaut mieux considérer et chercher n (que l'on ne connait pas, c'est donc ce qu'on appelle une inconnue, non ?) le plus petit possible pour l'inégalité soit vérifiée.

Ensuite avec la calculatrice (MENU STAT puis DIST puis BINM puis Bcd pour la casio), on obtient en saisissant X=116 puis n=135 puis p=0,9

et en saisissant X=116 puis n=134 puis p=0,9

Merci d'avoir résolu l'exo à la place de l'élève.

Encore faut-il savoir ce qu'il y a dans le programme de première S.....

:hum: Encore faut-il comprendre le programme de première S.....

Je ne sais quel était le but de l'ex, se servir de GEOGEBRA (sol 1) ou bien de la calculatrice (sol 2)

Personnellement, je pencherais pour l'utilisation de la calculette dans la recherche de l'inconnue n.
C'est ce que j'aurais conseillé à Mitch51.

quand à écrire une équation avec inconnue n, pour info comme il l'a été dit précédemment on est bien loin de ce que l'on demande en première S....

ah ?! on ne demande pas d'écrire sur son papier ce que l'on cherche avant de se lancer tête baissée sur la calculette ? Je pensais qu'écrire
>
était une formulation préalable du problème avant de se lancer dans la recherche à tâtons de n. C'est pas ce que vous avez fait ??

Certes, j'ai poussé le bouchon un peu loin (pour voir ce qu'il comprenait) en lui demandant d'écrire
Mais par ailleurs, une réponse miraculeuse d'une machine sur un calcul qu'un élève ne comprendrait pas ne me satisfait pas vraiment. Vous avez surement remarqué que Mitch51 s'est trompé dans la formule de la loi binomiale. C'était donc pas un mal de la revoir et de revenir sur les "fondamentaux".

[lecar]

>
S'il faut une calculatrice pour s'apercevoir que cette phrase a de très fortes chances d'être fausse, c'est que, à mon avis, l'élève manque sérieusement d'intuition et de bon sens (voir le 3ème message de cette discussion où Mitch51 comprend très bien que ce ne peut être ça).

C'est bien méconnaître l'ensemble des élèves qui sont dans la filière S dorénavant(je ne parle pas de celui qui a posé la question au départ) et les difficultés qui peuvent se présenter pour une grande partie d'entre eux avec des notions nouvelles....

Je peux vous répondre aussi que si le service clientèle ne veut pas de réclamations pour surbooking, on peut envisager p(X=117)=0,9 et ne pas pouvoir y parvenir....et oui, ce genre de réponse arrive est est correcte....

Merci d'avoir résolu l'exo à la place de l'élève.

La prochaine fois, modérez vos propos, cela m'évitera de faire ce genre de réponse pour clore la discussion....

:hum: Encore faut-il comprendre le programme de première S.....

Il y a ce qui est écrit et tout le reste (consignes des inspections, tendance pour le futur bac, niveau moyen des élèves.....) mais comme vous semblez être bien sur de vous et certainement le meilleur, peu de chance de vous convaincre...

Bon on dévie mais vous m'y avez contraint....

Cordialement,

J-F L