Bonjour à tous, je suis entrain de faire une analyse de fonction!
f(x) = 3xcarré -4 / (x-2)carré * (x+1)
Est ce Df est bien : R / (-1;2) soit Df = ) -inf ; -1(U)-1 ; 2(U)2; +inf(
Ensuite on me demande de dire si cette fonction est paire ou non, je me demande est ce qu'elle est toujours centré sur 0, du moins comment savoir si une fonction est centré sur 0 ! merci!
Analyse de fonction
9 messages
- Page 1 sur 1
Pour étudier sa limite, on va modifier son expression en développant au dénominateur.
 \quad = \quad \frac{3x^2-4}{(x^2+4-4x)(x+1)} \quad = \quad \frac{3x^2-4}{x^3+x^2+4x+4-4x^2-4x} \quad = \quad \frac{3x^2-4}{x^3-3x^2+4})
Ensuite, tu sais que la limite d'une fraction rationnelle en l'infini est la limite du quotient de ses termes de plus haut degré. Donc :
 \quad = \quad \lim\nolimits_{x \to \infty}\quad \frac{3x^2-4}{x^3-3x^2+4} = \lim\nolimits_{x \to \infty}\frac{3x^2}{x^3})
Car le terme de plus haut degré du numérateur est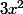 et celui du dénominateur est
et celui du dénominateur est  .
.
Or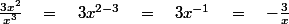 et
et 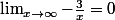 D'où
D'où  = 0)
Tu as compris ?
Ensuite, tu sais que la limite d'une fraction rationnelle en l'infini est la limite du quotient de ses termes de plus haut degré. Donc :
Car le terme de plus haut degré du numérateur est
Or
Tu as compris ?
Dans l'étude la parité de ta fonction, il existe un moyen très simple pour vérifier tes réponses.
Tu sais que si f est paire \quad = \quad f(x) \quad \quad) Prenons
Prenons 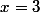 et vérifions :
et vérifions : =1 \quad \neq \quad f(3)=\frac{23}{4})
D'où, ta fonction n'est donc pas paire.
Tu sais que si f est impaire \quad = \quad -f(x)\quad) or on vient de voir que :
or on vient de voir que : =1 \quad \neq \quad -f(3)=-\frac{23}{4}) .
.
D'où, ta fonction n'est pas impaire.
Conclusion : la fonction n'est ni paire, ni impaire.
Tu sais que si f est paire
D'où, ta fonction n'est donc pas paire.
Tu sais que si f est impaire
D'où, ta fonction n'est pas impaire.
Conclusion : la fonction n'est ni paire, ni impaire.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
