Questions d'algèbre ...

[febula54]

Bonjour,
j'ai eu une liste d'exercice à faire mais je bloque pour l'un d'entre eux ... si vous pouviez m'aider...
voici l'énoncé :
Si G est un groupe abélien fini tel que|G|>2, alors Aut(G) est d'ordre pair

merci à vous

[jlb]

Bonsoir, une petite aide
considère
g:G-->G
x associe -x

que peux-tu dire de g ?( là tu as besoin de |G|>2) quel est son ordre dans Aut(G) muni de la composition?

[febula54]

Ah ok, donc je pose g : G -> G tel que g(x) = -x , et du coup j'ai que g g = Id, donc g est d'ordre 2. Du coup, par le théorème de classification des groupes abéliens finis je sais que Aut(G) est isomorphe à Zx ... et donc le cardinal de Aut() = cardinal de (Z) * le cardinal de (...) =2* ... .
C'est ça ?

[jlb]

plutôt théorème de Lagrange ({Id, g} sous groupe de Aut(G),. mais tu dois montrer que g endomorphisme bijectif) et tu as besoin de |G|>2 sinon g pourrait être l'identité ( dans Z2, x=-x)

[febula54]

Le théorème de Lagrange ? Lequel ... ?

Et comment est-ce que je sais que si |G|>2 alors il existe un élément qui n'est pas son propre inverse ?

[adrien69]

Ah ok, donc je pose g : G -> G tel que g(x) = -x , et du coup j'ai que g g = Id, donc g est d'ordre 2. Du coup, par le théorème de classification des groupes abéliens finis je sais que Aut(G) est isomorphe à Zx ... et donc le cardinal de Aut() = cardinal de (Z) * le cardinal de (...) =2* ... .
C'est ça ?

Attention ! Ce n'est pas parce que H=Z/aZ x Z/bZ x ... x Z/mZ que l'on a |H|=a^quelquechose ! Le cardinal est le produit des cardinaux. Pas l'un mis à une certaine puissance.
Et de toute façon le théorème de structure des groupes abéliens de type fini est un gros marteau dont on peut très souvent se passer. A fortiori quand il s'agit comme ici d'une propriété élémentaire sur les groupes.

(désolé d'être intervenu jlb, mais c'est une faute grave ça)

[febula54]

Ah oui non pardon je voulais mettre x mais je sais pas pourquoi j'ai mis * ... mais je voulais bien dire "fois" et non pas puissance. Bah je sais pas mais je suis dans le chapitre lié à ce théorème donc je pensais que je devrai l'utiliser ... ?

[adrien69]

Autant pour moi alors ^^ (et pas au temps)

(Mais fais ce que jlb t'a dit, il a raison)

[febula54]

Juste une question, je comprends pas l'existence d'un x qui ne soit pas son propre inverse. Si je prends G = le groupe de Klein, alors j'ai que le cardinal de G vaut 4, le groupe est abélien mais pourtant chacun des éléments est son propre inverse non ... ?

[jlb]

oui,oui tu as raison, en fait, en lisant l'énoncé j'ai été guidé par cette idée mais elle n'est valable que lorsque les éléments de G différents du neutre ne sont pas tous d'ordre 2.
et donc ...je ne vois pas comment t'aider, il reste ce cas à traiter.
bon courage.

[jlb]

en fait si!!! si tous les éléments sont d'ordre deux, tu en choisis un particulier a diff du neutre et tu considères x-->a + x ( c'est bien un automorphisme et ce n'est pas l'identité car il y a un autre élément dans G) et tu as bien g²(x)=a+a+x=x ouf!! et tu reprends la même conclusion.

donc dans tous les cas considérés, 2 divise l'ordre de Aut(G)

[adrien69]

Pourquoi vous vous emmerdez ? Si tous les éléments sont d'ordre 2, bah tous les éléments sont d'ordre 2 ? Et puis il suffit de considérer l'automorphisme intérieur (par conjugaison) donné par un élément d'ordre 2.

Le tout étant de savoir qu'il existe un élément d'ordre deux. Tant mieux s'il y en a plein.

[jlb]

cela ne convient pas, c'est l'identité puisque le groupe est abélien.

[adrien69]

Arf oui oups... C'est pour ça que tu le fais opérer à gauche... Ok. Pardon.

[jlb]

pas plus! c'était ma mauvaise idée: ce n'est qu'une bijection dans ce cas. par contre j'ai pensé à une sorte de transposition g(a)=b, g(b)=a, g(ab)=ab, g(c)=c,g(ac)=bc,g(bc)=ac,g(abc)=abc...(ça marche pour le groupe de Klein) mais je ne suis pas sur de moi pour notre G particuliers.. le th de fébula doit être utile pour traiter ce cas .

Mais je ne connais pas le théorème évoqué par fébula ( je n'ai qu'un très petit niveau mathématique mais je suis curieux ). que permet-il d'écrire si tous les éléments autres que le neutre sont d'ordre 2? car je soupçonne que cela justifie l'idée de mon automorphisme. si une âme charitable a ces connaissances, je l'en remercie grandement.

[adrien69]

Ok j'ai eu une idée grâce à vos machins.

Si |G|=2, les bijections de G dans G sont des automorphismes (identité et une transposition), donc c'est pair.

Si |G|>3 on considère comme jlb l'avait suggéré
Comme G est abélien, c'est bien un morphisme de groupe.

Or |G|>3, s'il existe un élément qui n'est pas d'ordre 1 ou 2 dans G, n'est pas l'identité et le théorème de Lagrange assure alors le résultat.

Supposons désormais que alors pour un certain q et (ça c'est trivial mais tu peux utiliser ton théorème pour le montrer).

On peut alors utiliser l'idée de jlb et faire permuter les 1 et les 0 :


g n'est pas l'identité de manière triviale, et g²=id.

Et dans les deux cas le théorème de Lagrange (l'ordre de tout sous-groupe, ici élément, divise l'ordre du groupe) permet de conclure.

[febula54]

Le théorème de classification des groupes abéliens finis te dit que si tu as G qui est un groupe abélien fini, alors il existe des entiers naturels … tels que … et est isomorphe à ….

Ici dans le cas où tout les éléments sont d'ordre 2, on sait que les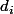 seront des puissances de 2. Le fait est que si tu as un 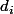qui vaut 4, alors ça sous-entend que ton possède un élément d'ordre 4, mais toi tu sais que tout tes éléments sont d'ordre 2, tu ne peux pas donc pas avoir un de tes 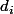qui vaut 4, de même pour toutes les puissances de 2 excepté pour
Donc tu en déduis que ton groupe est isomorphe à …, mais après je sais pas quoi faire...


J'ai eu une idée mais je sais pas si ça joue, je me suis rappelé que pour isomorphe à …, on a que est isomorphe à , or , donc comme ici on a , pour p=2 on a et donc Aut(G) est pair. Si quelqu'un pouvait contrôler ...

[adrien69]

Ça marche mais sinon je venais de le résoudre, y a personne qui m'écoute ? :soupir2:

En plus tu utilises de bien gros résultats pour cet exo je trouve...

[febula54]

Ah pardon j'écrivais le message en même temps que tu as dû poster le tiens.

Bah le problème c'est que pour moi, l'application g(x) = x+1 mod 2 c'est la même que g(x) = ax mais en notation additive. Parce qu'après pour moi l'application n'est pas un homomorphisme car g(x+y)=x+y+1 mod 2, alors que g(x)+g(y)=x+1 mod 2+y+1 mod 2, et donc g(x)+g(y)=x+y ...

En fait les éléments que j'ai utilisé sont des exercices qui étaient juste avant celui-ci ^^

[adrien69]

Ah pardon j'écrivais le message en même temps que tu as dû poster le tiens.

Bah le problème c'est que pour moi, l'application g(x) = x+1 mod 2 c'est la même que g(x) = ax mais en notation additive. Parce qu'après pour moi l'application n'est pas un homomorphisme car g(x+y)=x+y+1 mod 2, alors que g(x)+g(y)=x+1 mod 2+y+1 mod 2, et donc g(x)+g(y)=x+y ...

En fait les éléments que j'ai utilisé sont des exercices qui étaient juste avant celui-ci ^^

Nan vu que j'ai décomposé en produit de Z/2Z, je me retrouve en fait avec des transpositions sur chaque groupe du produit : et là je prends la tansposition naturelle.

Tu vois ce que je veux dire ?

Dans Z/2Z l'opération qui échange 1 et 0 est bien l'addition de 1. Ça c'est bien un morphisme.