Comparer des quotients

par **kevin1490** » 10 Avr 2013, 18:31

Bonjours, voilà je dois comparer 2 quotients et je n'y arrives pas cela fait 2 jours que je suis deçu, j'aimerai donc avoir des explications en sachant qu'il faut appliquer les produits remarquables. Merci

(a+b)²/a²-b²
et
a²+b²/(a-b)²

par **Corenn** » 10 Avr 2013, 18:35

kevin1490 a écrit:Bonjours, voilà je dois comparer 2 quotients et je n'y arrives pas cela fait 2 jours que je suis deçu, j'aimerai donc avoir des explications en sachant qu'il faut appliquer les produits remarquables. Merci

(a+b)²/a²-b²
et
a²+b²/(a-b)²

Bonjour Kevin,

Pourrais tu simplifier ton premier quotient en utilisant les identités remarquables?

je te conseilles de ne pas toucher au second quotient.

par **kevin1490** » 10 Avr 2013, 18:38

a²+2ab+b²/(a+b)(a-b)

par **Corenn** » 10 Avr 2013, 18:42

kevin1490 a écrit:a²+2ab+b²/(a+b)(a-b)

Ok oui c'est ça, mais en fait tu n'as pas besoin de développer le numérateur.

Si tu le laisses sous la forme

, il y a des choses qui se simplifient.

par **kevin1490** » 10 Avr 2013, 18:49

excusez moi mais je suis vraiment dépassé.
je crois avoir besoin de remise a niveau en math

par **Corenn** » 10 Avr 2013, 18:50

kevin1490 a écrit:excusez moi mais je suis vraiment dépassé.
je crois avoir besoin de remise a niveau en math

Ne t'inquiètes pas, l'exercice est compliqué.

Est ce que tu es d'accord que ton premier quotient s'écrit aussi comme ça?

par **kevin1490** » 10 Avr 2013, 18:58

(a+b)/(a-b)

par **kevin1490** » 10 Avr 2013, 19:02

mon premier quotient peut s écrire aussi (a+b)(a+b)= (a+b)² c est sa????

par **Archibald** » 10 Avr 2013, 19:26

Le numérateur de ton premier quotient tu veux dire. La réponse est oui puisque

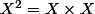
avec X=a+b

par **kevin1490** » 10 Avr 2013, 19:43

donc mon premier quotient serait
(a+b)/(a-b)
et mon second doit changé vu que l on met les 2 quotient au même dénominateur

par **chan79** » 10 Avr 2013, 20:17

kevin1490 a écrit:donc mon premier quotient serait
(a+b)/(a-b)
et mon second doit changé vu que l on met les 2 quotient au même dénominateur

tu peux mutiplier (a+b)/(a-b) en haut et en bas par (a-b)

par **kevin1490** » 10 Avr 2013, 20:39

donc enfin je peux comparer mes 2 quotient car ils ont le même dénominateur
donc

[quote]a²-b²/(a-b)² < a²+b²/(a-b)²

par **kevin1490** » 10 Avr 2013, 20:44

donc enfin je peux comparer mes 2 quotient car ils ont le même dénominateur
donc

a²-b²/(a-b)² < a²+b²/(a-b)²

par **kevin1490** » 10 Avr 2013, 21:40

donc enfin je peux comparer mes 2 quotient car ils ont le même dénominateur
donc

a²-b²/(a-b)² < a²+b²/(a-b)²

par **chan79** » 10 Avr 2013, 22:13

kevin1490 a écrit:donc enfin je peux comparer mes 2 quotient car ils ont le même dénominateur
donc

a²-b²/(a-b)² < a²+b²/(a-b)²

c'est bien ça

Comparer des quotients

Comparer des quotients

Qui est en ligne