Démonstration fonction dérivable
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mliebert
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Fév 2013, 19:25
-
 par mliebert » 31 Mar 2013, 18:03
par mliebert » 31 Mar 2013, 18:03
Bonjour,
J'ai commencé un exercice, mais je suis bloqué dès la première question qui est :
"Montrer que pour tout couple (a,b) de réels vérifiant aphi(a), il existe au moins un reel l appartenant à [a,b] vérifiant phi(l)=phi(a) et phi'(l)>=0. Indication : on pourra considérer un élément particulier de lensemble A des x appartenant à [a,b] tels que phi(x)<=phi(a)".
Merci par avance de vos réponses.
Cordialement .
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 31 Mar 2013, 19:41
par adrien69 » 31 Mar 2013, 19:41
Salut,
Tu sais que
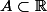
est non vide (a y appartient), tu sais qu'il est majoré par b (car inclus dans le segment [a,b] ), ça te donne envie de considérer quel élément de A ?
-
mliebert
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Fév 2013, 19:25
-
 par mliebert » 31 Mar 2013, 19:47
par mliebert » 31 Mar 2013, 19:47
Est-ce que c'est b-a?
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 31 Mar 2013, 19:56
par adrien69 » 31 Mar 2013, 19:56
Aouch.
Nein, tu ne sais même pas si il est dans ton segment celui-là (d'ailleurs c'est un petit exo de terminale rigolo de savoir quand il y est)
Je t'ai donné toutes les hypothèses qui te permettent de dire que quel élément de A existe ?
-
mliebert
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Fév 2013, 19:25
-
 par mliebert » 31 Mar 2013, 21:19
par mliebert » 31 Mar 2013, 21:19
Je suis perdu là :(
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 31 Mar 2013, 21:22
par adrien69 » 31 Mar 2013, 21:22
Faut prendre la borne sup' mein herr.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 110 invités
