[TS] Nombre Complexe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
gohan59750
- Membre Naturel
- Messages: 15
- Enregistré le: 14 Mar 2013, 17:05
-
 par gohan59750 » 24 Mar 2013, 20:12
par gohan59750 » 24 Mar 2013, 20:12
Bonsoir ! J'ai un petit exercice sur lequel je bloque et il est pour demain

Vous pourriez m'aider ?
On veut résoudre :
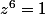
. Verifier que
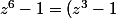(z^3+1))
. En utilisant les propriétés de la fonction cube, résoudre l'equation demandée
Pour la vérification c'est fait :
(z^3 +1)<br />=z^6 + z^3 - z^3 -1<br />=z^6 - 1)
C'est la suite qui me bloque..
Voilà merci de vos réponses

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 24 Mar 2013, 20:14
par fatal_error » 24 Mar 2013, 20:14
slt,
pour factoriser z^3-1, tu remarques 1 est racine évidente.
donc z^3-1 = (z-1)(az^2+bz+c), tu trouves a,b,c
idem z^3+1, -1 est évidente, donc z^3+1=(z+1)(dz^2+ez+f) et tu trouves d,e,f
edit: sinon, tu peux regarder les racines 3eme de 1 ou -1, je sais pas si c au programme
la vie est une fête

-
gohan59750
- Membre Naturel
- Messages: 15
- Enregistré le: 14 Mar 2013, 17:05
-
 par gohan59750 » 24 Mar 2013, 20:21
par gohan59750 » 24 Mar 2013, 20:21
Bonsoir ! Pour
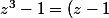(az^2 + bz + c))
Je trouve a = 1 b = 1 et c = 1 ..
Pour
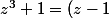(dz^2 + ez + f))
Je trouve d = 1 e = -1 et f = 1
Mais j'en fais quoi de ça ?


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 24 Mar 2013, 20:43
par chan79 » 24 Mar 2013, 20:43
gohan59750 a écrit:Bonsoir ! Pour
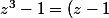(az^2 + bz + c))
Je trouve a = 1 b = 1 et c = 1 ..
Pour
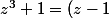(dz^2 + ez + f))
Je trouve d = 1 e = -1 et f = 1
Mais j'en fais quoi de ça ?

salut
tu as
a³-b³=(a-b)(a²+ab+b²)
a³+b³=(a+b)(a²-ab+b²)
-
gohan59750
- Membre Naturel
- Messages: 15
- Enregistré le: 14 Mar 2013, 17:05
-
 par gohan59750 » 24 Mar 2013, 20:52
par gohan59750 » 24 Mar 2013, 20:52
chan79 a écrit:salut
tu as
a³-b³=(a-b)(a²+ab+b²)
a³+b³=(a+b)(a²-ab+b²)
Bonsoir !
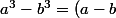(a^2+ab+b^2))
ça donne :
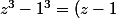(z^2-z+1))
Et
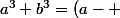(a^2-ab+b^2))
ça donne :
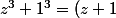(z^2+z+1))
C'est ça ?
Et du coup, je peux resoudre
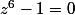
mais pour
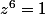
?
-
gohan59750
- Membre Naturel
- Messages: 15
- Enregistré le: 14 Mar 2013, 17:05
-
 par gohan59750 » 24 Mar 2013, 23:28
par gohan59750 » 24 Mar 2013, 23:28
Pour

Les solutions sont -1 ; 1 ; i et -i C'est bien ça ?
Mais pour

je vois pas


-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 24 Mar 2013, 23:38
par fatal_error » 24 Mar 2013, 23:38
je pense qu'il te manque des solutions pour z^6-1=0, et puis i^6=-1 qui est pas solution..
et sinon, z^6-1=0 <=> z^6=1 ... donc les solutions de l'égalité de gauche sont les mêmes que celle de droite, et vice versa
la vie est une fête

-
gohan59750
- Membre Naturel
- Messages: 15
- Enregistré le: 14 Mar 2013, 17:05
-
 par gohan59750 » 24 Mar 2013, 23:54
par gohan59750 » 24 Mar 2013, 23:54
fatal_error a écrit:je pense qu'il te manque des solutions pour z^6-1=0, et puis i^6=-1 qui est pas solution..
et sinon, z^6-1=0 z^6=1 ... donc les solutions de l'égalité de gauche sont les mêmes que celle de droite, et vice versa
z-1 = 0
z = 1
z+1=0
z = -1
Pour z²-z+1
Delta = -3
Solutions :

Pour z²+z+1
Delta = -3
Solutions :

Donc les solutions de
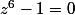
sont : S = {

} Donc ce sont les mêmes pour
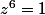
-
chris06
- Membre Naturel
- Messages: 29
- Enregistré le: 08 Fév 2013, 22:19
-
 par chris06 » 25 Mar 2013, 03:02
par chris06 » 25 Mar 2013, 03:02
Pour z²-z+1
Delta = -3
Solutions :

d'accord avec toi
Pour z²+z+1
Delta = -3
Solutions :

un peu moins la, petite erreur de signe quelque part non?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 25 Mar 2013, 08:26
par chan79 » 25 Mar 2013, 08:26
gohan59750 a écrit:Bonsoir !
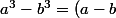(a^2+ab+b^2))
ça donne :
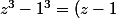(z^2-z+1))
Et
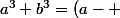(a^2-ab+b^2))
ça donne :
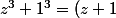(z^2+z+1))
C'est ça ?
Attention, erreur de signe
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 94 invités