Suite , fonction

par **EinsteinE=mc2** » 18 Mar 2013, 00:53

bonjour,

Voici un exo sur les suites : Soit (Un) définie par u0=1 et pour tous n appartenant a N Un+1 = ( Un + 8) /( Un+3)

On pose f(x)= x+8 / x+3

1) donner le tableau de variations de f
2) Montrer que pour tout n appartenant a N 1=< Un =< 4
3) Etudier (U2n) et (U2n+1)
4) Conclure sur la convergence de (Un)

Donc j'ai reussis a faire la question 1)

Pour la 1) je trouve que f est décroissante de - l'infini a + l'infini avec une valeur interdite en -3
lim f(x) quand x tend vers +/- l'infini = 1

Pour la 2) je bloque :hein: j'ai essayer le raisonnement par récurrence mais pour l'hérédité je suis bloquer
je suppose que la propriété est vrai au rang n on a donc :

1=< Un =< 4

et pour retrouvé Un+1 jbeug :/

Merci d'avance pour votre aide .

par **capitaine nuggets** » 18 Mar 2013, 08:17

Salut !

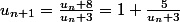EinsteinE=mc2 a écrit:bonjour,

Voici un exo sur les suites : Soit (Un) définie par u0=1 et pour tous n appartenant a N Un+1 = ( Un + 8) /( Un+3)

On pose f(x)= x+8 / x+3

1) donner le tableau de variations de f
2) Montrer que pour tout n appartenant a N 1=< Un =< 4
3) Etudier (U2n) et (U2n+1)
4) Conclure sur la convergence de (Un)

Donc j'ai reussis a faire la question 1)

Pour la 1) je trouve que f est décroissante de - l'infini a + l'infini avec une valeur interdite en -3
lim f(x) quand x tend vers +/- l'infini = 1

Pour la 2) je bloque :hein: j'ai essayer le raisonnement par récurrence mais pour l'hérédité je suis bloquer
je suppose que la propriété est vrai au rang n on a donc :

1=< Un =< 4

et pour retrouvé Un+1 jbeug :/

Merci d'avance pour votre aide .

:++:

par **EinsteinE=mc2** » 18 Mar 2013, 09:11

1< Un <4 => 4< Un+3 <7 => 1/7 < 1/Un+3 < 1/4
=> 5/7 + 7/7 < 5/ Un+3 + 1 < 5/4 + 4/4
=> 13/7 < Un+1 < 9/4 ?!!!

par **EinsteinE=mc2** » 18 Mar 2013, 09:47

=> 1<13/7< Un+1 < 9/4 < 4
=> 1< Un+1< 4

Voila j'ai montré que la propriété était vrai au rang n+ 1

par **chan79** » 18 Mar 2013, 10:05

EinsteinE=mc2 a écrit:1 4 1/7 5/7 + 7/7 13/7 < Un+1 < 9/4 ?!!!

salut
on suppose

on trouve

(égalités 1)

(égalités 2)

comme des nombres positifs sont rangés dans l'ordre contraire à celui de leurs inverses:

(égalités 3)

on multiplie membre à membre les inégalités 1 et 3

et

par **EinsteinE=mc2** » 18 Mar 2013, 10:15

Besoin d'aide pour la question 3 je bloque totalement ....! :mur: :mur: :mur:

Suite , fonction

Suite , fonction

helpp étudier U2n et U2n+1

Qui est en ligne