Bonjour à tous,
J'ai un exercice sur les logarithmes à effectuer, et je ne vois pas trop comment m'y prendre...
Montrer que pour tout x réel de l'intervalle ]0;1[ on a : (xlnx)/(x²-1) < ou égale à 1/2
Es ce que je dois factoriser ou dériver ?
Merci d'avance pour votre aide.
Logarithmes (TS)
10 messages
- Page 1 sur 1
[quote="Heyou"]Bonjour à tous,
J'ai un exercice sur les logarithmes à effectuer, et je ne vois pas trop comment m'y prendre...
Montrer que pour tout x réel de l'intervalle ]0;1[ on a : (xlnx)/(x²-1) 0
Tu poses f(x) = xln(x) - (x²-1)/2 est tu étudies les variations de cette fonction. Tu seras amené à calculer la dérivée seconde pour déterminer le signe de la dérivée. Essaie et si tu bloques tu reviens
J'ai un exercice sur les logarithmes à effectuer, et je ne vois pas trop comment m'y prendre...
Montrer que pour tout x réel de l'intervalle ]0;1[ on a : (xlnx)/(x²-1) 0
Tu poses f(x) = xln(x) - (x²-1)/2 est tu étudies les variations de cette fonction. Tu seras amené à calculer la dérivée seconde pour déterminer le signe de la dérivée. Essaie et si tu bloques tu reviens
raph107 a écrit:Je ne vois pas comment tu peux factoriser. Il faut dériver mais avant il faut transformer l'inégalité de façon à avoir une fonction plus simple à étudier.
x²-1 0
Tu poses f(x) = xln(x) - (x²-1)/2 est tu étudies les variations de cette fonction. Tu seras amené à calculer la dérivée seconde pour déterminer le signe de la dérivée. Essaie et si tu bloques tu reviens
c'est le tout divisé par 2 ?
Je ne suis vraiment pas sur de mon résultat mais..
je trouve f'(x) = lnx + 1 - (4x-2)/4 :hein:
Heyou a écrit:c'est le tout divisé par 2 ?
Je ne suis vraiment pas sur de mon résultat mais..
je trouve f'(x) = lnx + 1 - (4x-2)/4 :hein:
Je détaille le début.
(xlnx)/(x²-1) = 0
Je pose f(x) = xln(x) - (1/2)(x²-1)
f'(x) = ln(x) + 1 -(1/2)(2x) = ln(x) - x + 1.
Tu calcules f''(x), tu trouveras que f''(x) > 0 sur ]0;1[, tu en déduiras que f' est croissante et en calculant f'(1) tu déduiras que f' est négative donc f décroissante et tu concluras en calcualant f(1).
D'accord ! Merci beaucoup pour le développement, j'ai compris ! :we:
Je file terminer tout ça !
Sinon,j'ai un second exercice, j'ai les idées mais ne suis pas certaine de moi...
voici l'énoncé :
1)Prouver que pour tout réel x > 0 on a :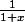
 ln (1+x) - lnx
ln (1+x) - lnx 

2) Déterminer la limite de la suite (Un) définie par Un =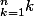 1/k pour tout n entier naturel.
1/k pour tout n entier naturel.
Pour le 1)
Je pensais à dire que f(x) =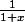
g(x) = ln (1+x) - lnx
h(x) =
Puis de comparer g(x) - h(x)
Je trouve ensuite que g(x) < h(x)
Mais pour la suite, je bloque.
Je file terminer tout ça !
Sinon,j'ai un second exercice, j'ai les idées mais ne suis pas certaine de moi...
voici l'énoncé :
1)Prouver que pour tout réel x > 0 on a :
2) Déterminer la limite de la suite (Un) définie par Un =
Pour le 1)
Je pensais à dire que f(x) =
g(x) = ln (1+x) - lnx
h(x) =
Puis de comparer g(x) - h(x)
Je trouve ensuite que g(x) < h(x)
Mais pour la suite, je bloque.
[quote="Heyou"]D'accord ! Merci beaucoup pour le développement, j'ai compris ! :we:
Je file terminer tout ça !
Sinon,j'ai un second exercice, j'ai les idées mais ne suis pas certaine de moi...
voici l'énoncé :
1)Prouver que pour tout réel x > 0 on a :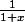
 ln (1+x) - lnx
ln (1+x) - lnx 

2) Déterminer la limite de la suite (Un) définie par Un =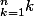 1/k pour tout n entier naturel.
1/k pour tout n entier naturel.
Pour le 1)
Je pensais à dire que f(x) =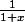
g(x) = ln (1+x) - lnx
h(x) =
Puis de comparer g(x) - h(x)
Je trouve ensuite que g(x) = 0 ce qui montrera la double inégalité.
Pour la 2) il y a certainement un pb de transcription
Je file terminer tout ça !
Sinon,j'ai un second exercice, j'ai les idées mais ne suis pas certaine de moi...
voici l'énoncé :
1)Prouver que pour tout réel x > 0 on a :
2) Déterminer la limite de la suite (Un) définie par Un =
Pour le 1)
Je pensais à dire que f(x) =
g(x) = ln (1+x) - lnx
h(x) =
Puis de comparer g(x) - h(x)
Je trouve ensuite que g(x) = 0 ce qui montrera la double inégalité.
Pour la 2) il y a certainement un pb de transcription
raph107 a écrit:Pose plutot: f(x) = ln(1+x) - ln(x) - 1/x et g(x) = ln(1+x) - ln(x) - 1/(x+1)
En étudiant le sens de variation de f et g tu déduiras que f(x) = 0 ce qui montrera la double inégalité.
Pour la 2) il y a certainement un pb de transcription
D'accord ! Je n'y avais pas pensé. Merci beaucoup, j'ai vraiment du mal avec les logarithmes...
Pour la 2) j'ai oublié à la fin de la question que c'est un entier naturel non nul
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
