Probabilité !
21 messages
- Page 1 sur 2 - 1, 2
Probabilité !
coucou, j'ai un exo qui parait bete mais plus j'y reflechi plus je m'embrouille
2 jouers A et B lancent chacun n pieces de monnaie, la probabilité de tirer face est pour chaque piece p=1/2 (jusqu'a la tt va bien !!)
Soit X le nombre de faces tirées par A
Y B
Calculer les probabilités de evenements :
X=Y ; X strictement supérieur à Y
2 jouers A et B lancent chacun n pieces de monnaie, la probabilité de tirer face est pour chaque piece p=1/2 (jusqu'a la tt va bien !!)
Soit X le nombre de faces tirées par A
Y B
Calculer les probabilités de evenements :
X=Y ; X strictement supérieur à Y
si l'important pour nous c'est le nombre de face tirés voila la solution ,sauf si c'est mon jour
chaque joueur a possibilité
possibilité
tirer face.
face.
par suite le nombre de possiblité pour les resultats des deux joueur est^2)
pour X=Y, il a possibilité,
possibilité, 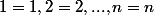
donc P(X=Y)=(nombre de possiblité pour avoire X=Y)/(nombre de possibilité totale)=^2}=\frac{1}{n+1})
chaque joueur a
tirer
par suite le nombre de possiblité pour les resultats des deux joueur est
pour X=Y, il a
donc P(X=Y)=(nombre de possiblité pour avoire X=Y)/(nombre de possibilité totale)=
aviateurpilot a écrit:chaque joueur a n+1 possibilité
tirer 0,1,2,...,n-1 \ ou \ n face.
par suite le nombre de possiblité pour les resultats des deux joueur est (n+1)^2
Ba oui mais il me semble bien que ces possibilités ne sont pas équiprobables, on a plus de chance d'avoir un résultat proche de n/2 que de 0 par exemple (n>4) et on ne peut pas alors se contenter de dénombrer les cas d'égalité comme tu le fais, non ?
mon raisonnement :
Comme l'a dit mpo on a P(X=Y=k) = (P(X=k))²
Tous les cas où X=Y sont : X=Y=0, X=Y=1, ... X=Y=n
La probabilité P(X=Y) est la somme des probabilités P(X=Y=1) + P(X=Y=2) + ... + P(X=Y=n), c'est-à-dire somme des P(X=Y=k) pour toutes les valeurs de k.
mpo a écrit:pour tout k de N, on a :
P(X=Y=k) = P(X=k et Y=k) = P(X=k) P(Y=k) car X et Y sont indépendantes puisque le tirage du joueur A est independant de celui du joueur B
avec X et qui suivent une Binomiale de paramètres (n,p=1/2)
Comme l'a dit mpo on a P(X=Y=k) = (P(X=k))²
Tous les cas où X=Y sont : X=Y=0, X=Y=1, ... X=Y=n
La probabilité P(X=Y) est la somme des probabilités P(X=Y=1) + P(X=Y=2) + ... + P(X=Y=n), c'est-à-dire somme des P(X=Y=k) pour toutes les valeurs de k.
Le raisonnement est très simple :
A tire x faces et n-x piles
B tire y faces et n-y piles
J'inverse les résultats de B en transformant les piles en face et vice versa
On est bien d'accord sur le fait que la proba de tirer y face pour B est identique à celle de tirer n-y face.
Maintenant je réunis les résultats (après inversion):
le nombre total de piles sera n-x+y et celui de faces n-y+x
Pour satisfaire ma condition, il faut que x=y, ce qui correspond à un tirage global de n piles ou faces sur 2n.
On peut présenter ça autrement....
Sans inversion : Prob(Y=y)=Prob(Y=n-y)=Prob(N-Y=y)
On réécrit le problème : A lance n pièces et obtient x faces. Ensuite B lance n pièces. Quelle est la probabilité qu'il obtienne n-x faces.
C'est bien sur la même chose qu'un seul tirage qui donne n face :id:
A tire x faces et n-x piles
B tire y faces et n-y piles
J'inverse les résultats de B en transformant les piles en face et vice versa
On est bien d'accord sur le fait que la proba de tirer y face pour B est identique à celle de tirer n-y face.
Maintenant je réunis les résultats (après inversion):
le nombre total de piles sera n-x+y et celui de faces n-y+x
Pour satisfaire ma condition, il faut que x=y, ce qui correspond à un tirage global de n piles ou faces sur 2n.
On peut présenter ça autrement....
Sans inversion : Prob(Y=y)=Prob(Y=n-y)=Prob(N-Y=y)
On réécrit le problème : A lance n pièces et obtient x faces. Ensuite B lance n pièces. Quelle est la probabilité qu'il obtienne n-x faces.
C'est bien sur la même chose qu'un seul tirage qui donne n face :id:
aviateurpilot a écrit:non, il y a une équiprobabilité.
la probabilité de tirer face est pour chaque piece p=1/2
Bonsoir aviateur,
quand je dis qu'il n'y a pas équiprobabilité et donc que ta méthode ne marche pas, il ne s'agit évidement pas de la probabilité d'avoir pile ou face (bien sur c'est 1/2). Je te parle de la probabilité d'avoir par exemple 3 faces sur les n tirage n'est pas du tout la même que d'avoir 10 faces sur les n tirages. Et donc quand tu denombres les cas :
aviateurpilot a écrit:chaque joueur a n+1 possibilité tirer 0,1,2,...,n-1 \ ou \ n face.
par suite le nombre de possiblité pour les resultats des deux joueur est (n+1)^2
donc P(X=Y)=(nombre de possiblité pour avoire X=Y)/(nombre de possibilité totale)=
tu omets le fait que ces évènements ne sont pas équiprobables (P(X=Y=0)
tize a écrit:Bonsoir aviateur,
quand je dis qu'il n'y a pas équiprobabilité et donc que ta méthode ne marche pas, il ne s'agit évidement pas de la probabilité d'avoir pile ou face (bien sur c'est 1/2). Je te parle de la probabilité d'avoir par exemple 3 faces sur les n tirage n'est pas du tout la même que d'avoir 10 faces sur les n tirages
merci tize, j'ai compris mtn
joselechaud a écrit:enfin aviateur pilot reflechit un peu a l'absurdité de ton raisonnement !!
oups, tu n'as rien dit !!
______________________________________
aviateurpilot a écrit:si l'important pour nous c'est le nombre de face tirés voila la solution ,
moi j'ai supposer que:
sinon la solution de Sdec25 est vraie
Petit complément :
On peut retrouver assez simplement le passage de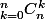^2=C_{2n}^{n}\)
il faut établir la formule plus générale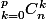 \;(C_{m}^{p-k}\)=C_{n+m}^{p}\)
en développant^n \; (1+u)^m \;=(1+u)^{n+m}) en appliquant la formule du binôme à chacun des trois termes
en appliquant la formule du binôme à chacun des trois termes
Puis en regroupant des termes selon le degré de u dans le premier membre
Et enfin en identifiant les termes de même degré
Il suffit ensuite de faire m=n=p et d'utiliser la relation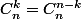
On peut retrouver assez simplement le passage de
il faut établir la formule plus générale
en développant
Puis en regroupant des termes selon le degré de u dans le premier membre
Et enfin en identifiant les termes de même degré
Il suffit ensuite de faire m=n=p et d'utiliser la relation
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
