Endomorphisme orthogonal, matrice de passag
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
par chelsea-asm » 13 Mar 2013, 23:05
Bonsoir,
Je n'arrive pas à déterminer une matrice de passage d'une base orthonormée dans une autre.
J'ai
)
une bon directe de
, ev euclidien de dim 2.
Soit
)
une base, telle que
et
\epsilon_1 + sin(\theta)\epsilon_2)
Avec
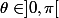
différent de
Soit l un endomorphisme de E de matrice
dans la base
(je n'arrive pas à mettre le LaTex pour la matrice) :
)
l est un endomorphisme orthogonal car j'ai montré qu'il conserve la norme
||^2)
Avec
Comment puis-je déterminer la matrice de passage de la base
)
à la base
?
J'ai essayé avec les valeurs propres et sous-espaces propres comme pour la diagonalisation, mais ça semble ne pas être la bonne méthode. Merci pour vos réponses !
Cordialement.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
par XENSECP » 13 Mar 2013, 23:14
Il faut inverser les équations
et
.
v_1 + sin(\theta)\epsilon_2 \Leftrightarrow \epsilon_2 = -\frac{1}{\tan{\theta}}v_1 + v_2)
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
par chelsea-asm » 13 Mar 2013, 23:20
D'accord !
D'autres m'ont proposé
\\0&\sin(\theta)\end{pmatrix})
Mais c'est le cas que si (v1,v2) est une bon ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
par XENSECP » 13 Mar 2013, 23:24
Au signe près ça me semble bien. Il suffit de multiplier par
mon expression et tu trouves ton deuxième vecteur.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
par chelsea-asm » 13 Mar 2013, 23:34
XENSECP a écrit:Au signe près ça me semble bien. Il suffit de multiplier par
mon expression et tu trouves ton deuxième vecteur.
Ok, ben j'ai compris alors ! Merci beaucoup !! Passe une bonne soirée
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
