Géométrie dans l'espace

par **chalut** » 09 Mar 2013, 15:10

Bonjour à tous,

J'ai un exercice à faire mais je bloque...

L'énoncé est :
L'espace est rapporté à un repère orthonormal (O;i;j;k).
On considère les points A(-1;3;1); B(3;1;-1); C(1;-3;-1); D(-5;0;2).
Justifier que ABC est un triangle rectangle.
Montrer que les vecteurs AB et CD sont colinéaires.
Montrer que A, B, C et D sont coplanaires. Quelle est la nature du quadrilatère ABCD ?

J'ai trouvé que AB²+BC²=44 et AC²=44. Donc d'après la réciproque du théorème de Pythagore, ABC est un triangle rectangle en B.
Ensuite, j'ai trouvé les coordonnées du vecteur AB : (4;-2;-2) et du vecteur CD : (-6;3;3). Donc vecteur AB= -3/2 * vecteur CD sont les vecteurs sont colinéaires.
Par contre maintenant je bloque pour montrer que les points A, B, C et D sont coplanaires.

Merci d'avance pour votre aide :)

par **siger** » 09 Mar 2013, 16:06

chalut a écrit:Bonjour à tous,

J'ai un exercice à faire mais je bloque...

L'énoncé est :
L'espace est rapporté à un repère orthonormal (O;i;j;k).
On considère les points A(-1;3;1); B(3;1;-1); C(1;-3;-1); D(-5;0;2).
Justifier que ABC est un triangle rectangle.
Montrer que les vecteurs AB et CD sont colinéaires.
Montrer que A, B, C et D sont coplanaires. Quelle est la nature du quadrilatère ABCD ?

J'ai trouvé que AB²+BC²=44 et AC²=44. Donc d'après la réciproque du théorème de Pythagore, ABC est un triangle rectangle en B.
Ensuite, j'ai trouvé les coordonnées du vecteur AB : (4;-2;-2) et du vecteur CD : (-6;3;3). Donc vecteur AB= -3/2 * vecteur CD sont les vecteurs sont colinéaires.
Par contre maintenant je bloque pour montrer que les points A, B, C et D sont coplanaires.

Merci d'avance pour votre aide

une methode ( parmi d'autres)
determiner l'equation du plan ABC :
ecrire que les points A, B et C verifient l'equation du plan
ax + by + cz + d = 0
pour determiner les coefficients a,b,c et d et verifier que D est dans ce plan... ...

par **siger** » 09 Mar 2013, 16:12

chalut a écrit:Bonjour à tous,

J'ai un exercice à faire mais je bloque...

L'énoncé est :
L'espace est rapporté à un repère orthonormal (O;i;j;k).
On considère les points A(-1;3;1); B(3;1;-1); C(1;-3;-1); D(-5;0;2).
Justifier que ABC est un triangle rectangle.
Montrer que les vecteurs AB et CD sont colinéaires.
Montrer que A, B, C et D sont coplanaires. Quelle est la nature du quadrilatère ABCD ?

J'ai trouvé que AB²+BC²=44 et AC²=44. Donc d'après la réciproque du théorème de Pythagore, ABC est un triangle rectangle en B.
Ensuite, j'ai trouvé les coordonnées du vecteur AB : (4;-2;-2) et du vecteur CD : (-6;3;3). Donc vecteur AB= -3/2 * vecteur CD sont les vecteurs sont colinéaires.
Par contre maintenant je bloque pour montrer que les points A, B, C et D sont coplanaires.

Merci d'avance pour votre aide

les vecteurs AB et CD sont colineaires, mais ne passent pas par un point commun, ils sont donc paralleles......et deux vecteurs parallèles definissent UN plan

Pour le demontrer autrement, une methode ( parmi d'autres)
determiner l'equation du plan ABC :
ecrire que les points A, B, C et D verifient l'equation du plan
ax + by + cz + d = 0
pour determiner les coefficients a,b,c et d et verifier que le systeme des quatre equations admet une solution.......

par **siger** » 09 Mar 2013, 16:35

chalut a écrit:Bonjour à tous,

J'ai un exercice à faire mais je bloque...

L'énoncé est :
L'espace est rapporté à un repère orthonormal (O;i;j;k).
On considère les points A(-1;3;1); B(3;1;-1); C(1;-3;-1); D(-5;0;2).
Justifier que ABC est un triangle rectangle.
Montrer que les vecteurs AB et CD sont colinéaires.
Montrer que A, B, C et D sont coplanaires. Quelle est la nature du quadrilatère ABCD ?

J'ai trouvé que AB²+BC²=44 et AC²=44. Donc d'après la réciproque du théorème de Pythagore, ABC est un triangle rectangle en B.
Ensuite, j'ai trouvé les coordonnées du vecteur AB : (4;-2;-2) et du vecteur CD : (-6;3;3). Donc vecteur AB= -3/2 * vecteur CD sont les vecteurs sont colinéaires.
Par contre maintenant je bloque pour montrer que les points A, B, C et D sont coplanaires.

Merci d'avance pour votre aide

les deux vecteurs AB et CD sont colineaires sans points communs, ils sont donc paralleles et deux vecteurs paralleles definissent UN plan, ...'

une methode pour le demontrer analytiquement ( entre autres)
si le plan ABC defini par les vecteurs AB et AC contient D on doit avoir la relation vectoriielle
AD = a* AB + b* AC...

par **chalut** » 09 Mar 2013, 18:04

D'accord merci :)
Et après pour la nature de quadrilatére ABCD, on sait que ABC est un triangle rectangle et que AB et CD sont parallèles... mais ça ne nous permet pas de donner la nature de ABCD ?

par **capitaine nuggets** » 09 Mar 2013, 18:33

Salut !

chalut a écrit:D'accord merci
Et après pour la nature de quadrilatére ABCD, on sait que ABC est un triangle rectangle et que AB et CD sont parallèles... mais ça ne nous permet pas de donner la nature de ABCD ?

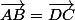signifie que (AB)//(DC) et AB=DC

par **siger** » 09 Mar 2013, 20:55

Re
AB et CD sont paralleles et de longueur inegales(rapport 3/2)
doncun quadrilatere qui a deux cotes opposes paralleles et inegaux est un .....

par **chalut** » 10 Mar 2013, 14:42

un trapèze ? Mais comment je le justifie ?

par **siger** » 10 Mar 2013, 17:11

C'est fait!
par definition un trapeze est un quadrilatere qui a deux cotes paralleles inegaux
(cotes egaux = parallelogramme ou losange ou rectanglr)

Géométrie dans l'espace

Géométrie dans l'espace

Qui est en ligne