Primitive
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Elise3
- Membre Naturel
- Messages: 17
- Enregistré le: 07 Mar 2013, 17:19
-
 par Elise3 » 07 Mar 2013, 17:22
par Elise3 » 07 Mar 2013, 17:22
Bonjour, j'aimerais un peu d'aide pour trouver la primitive de : (x^4 x arctan(x))/(x^2+1)
-
Erlinaewen
- Membre Naturel
- Messages: 27
- Enregistré le: 08 Fév 2013, 23:42
-
 par Erlinaewen » 07 Mar 2013, 18:09
par Erlinaewen » 07 Mar 2013, 18:09
Elise3 a écrit:Bonjour, j'aimerais un peu d'aide pour trouver la primitive de : (x^4 * arctan(x))/(x^2+1)
On a

et

devient la somme de produits de termes...
-
Elise3
- Membre Naturel
- Messages: 17
- Enregistré le: 07 Mar 2013, 17:19
-
 par Elise3 » 07 Mar 2013, 19:04
par Elise3 » 07 Mar 2013, 19:04
Erlinaewen a écrit:On a

et

devient la somme de produits de termes...
Désolée mais je ne comprends pas...
-
Erlinaewen
- Membre Naturel
- Messages: 27
- Enregistré le: 08 Fév 2013, 23:42
-
 par Erlinaewen » 07 Mar 2013, 19:24
par Erlinaewen » 07 Mar 2013, 19:24
Elise3 a écrit:Désolée mais je ne comprends pas...
Développe et distribue :

sur

puis intègre par parties...

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 07 Mar 2013, 19:34
par chan79 » 07 Mar 2013, 19:34
Elise3 a écrit:Bonjour, j'aimerais un peu d'aide pour trouver la primitive de : (x^4 x arctan(x))/(x^2+1)
on a aussi
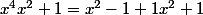
Ensuite, des IPP suffisent.
-
Elise3
- Membre Naturel
- Messages: 17
- Enregistré le: 07 Mar 2013, 17:19
-
 par Elise3 » 07 Mar 2013, 21:44
par Elise3 » 07 Mar 2013, 21:44
chan79 a écrit:on a aussi
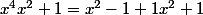
Ensuite, des IPP suffisent.
Dans mon calcul, je dois faire intervenir la primitive de arctan(x) j'intègre aussi par partie ?
-
raph107
- Membre Relatif
- Messages: 205
- Enregistré le: 17 Sep 2005, 08:53
-
 par raph107 » 07 Mar 2013, 23:33
par raph107 » 07 Mar 2013, 23:33
Elise3 a écrit:Dans mon calcul, je dois faire intervenir la primitive de arctan(x) j'intègre aussi par partie ?
Tu auras à integrer:
)
)
}{x^2+1})
la troisième est de la forme u'u et pour les 2 autres tu utilises une integartion par parties de façon à éliminer arctan
-
Elise3
- Membre Naturel
- Messages: 17
- Enregistré le: 07 Mar 2013, 17:19
-
 par Elise3 » 07 Mar 2013, 23:41
par Elise3 » 07 Mar 2013, 23:41
raph107 a écrit:Tu auras à integrer:
)
)
}{x^2+1})
la troisième est de la forme u'u et pour les 2 autres tu utilises une integartion par parties de façon à éliminer arctan
Je trouve
(\frac{1}{2} - \frac{x^{3}}{3}) + \arctan(x)(\frac{x^{4}}{3} - x) + \frac{1}{2}ln(1+x^{2}))
. Vous trouvez ça viable ?
-
raph107
- Membre Relatif
- Messages: 205
- Enregistré le: 17 Sep 2005, 08:53
-
 par raph107 » 08 Mar 2013, 00:20
par raph107 » 08 Mar 2013, 00:20
Elise3 a écrit:Je trouve
(\frac{1}{2} - \frac{x^{3}}{3}) + \arctan(x)(\frac{x^{4}}{3} - x) + \frac{1}{2}ln(1+x^{2}))
. Vous trouvez ça viable ?
Je n'ai pas le courage de faire les calculs, je fais appel à ma calculatrice qui donne:
[2ln(x²+1)]/3 + [(arctan(x)]²/2 +x(x²-3)arctan(x)/3 - x²/6

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Mar 2013, 08:57
par chan79 » 08 Mar 2013, 08:57
Elise3 a écrit:Je trouve
(\frac{1}{2} - \frac{x^{3}}{3}) + \arctan(x)(\frac{x^{4}}{3} - x) + \frac{1}{2}ln(1+x^{2}))
. Vous trouvez ça viable ?
Pour la primitive de x² arctan(x), on fait une IPP: u= arctan(x) et v'=x²
On trouve:
-\fra{1}{3}(\fra{x^2}{2}-\fra{1}{2} ln(1+x^2)))
-
Elise3
- Membre Naturel
- Messages: 17
- Enregistré le: 07 Mar 2013, 17:19
-
 par Elise3 » 08 Mar 2013, 11:16
par Elise3 » 08 Mar 2013, 11:16
chan79 a écrit:Pour la primitive de x² arctan(x), on fait une IPP: u= arctan(x) et v'=x²
On trouve:
-\fra{1}{3}(\fra{x^2}{2}-\fra{1}{2} ln(1+x^2)))
bizarre que je ne trouve pas pareil...J'ai pris u'=x^2 et v=arctan(x)
Au final,
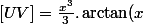 ;\; \int{UV'} = x^{2} . \frac{1}{x^{2}+1} = 1 - \frac{1}{x^{2}+1} ;\; F(UV') = x - \arctan(x))

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Mar 2013, 11:30
par chan79 » 08 Mar 2013, 11:30
Elise3 a écrit:bizarre que je ne trouve pas pareil...J'ai pris u'=x^2 et v=arctan(x)
Au final,
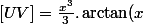 ;\; \int{UV'} = x^{2} . \frac{1}{x^{2}+1} = 1 - \frac{1}{x^{2}+1} ;\; F(UV') = x - \arctan(x))
v=arctan(x)
v'=1/(1+x²)
u'=x²
u=(x³)/3
)
-
Elise3
- Membre Naturel
- Messages: 17
- Enregistré le: 07 Mar 2013, 17:19
-
 par Elise3 » 08 Mar 2013, 13:56
par Elise3 » 08 Mar 2013, 13:56
chan79 a écrit:v=arctan(x)
v'=1/(1+x²)
u'=x²
u=(x³)/3
)
Ah oui j'avais oublié la primitive de u'...
J'ai une autre primitive à résoudre si ça vous dérange pas :
 = x\sqrt{x^{2} + x + 1})
Comment faire cette fois-ci ?
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 08 Mar 2013, 14:01
par jlb » 08 Mar 2013, 14:01
Elise3 a écrit:Ah oui j'avais oublié la primitive de u'...
J'ai une autre primitive à résoudre si ça vous dérange pas :
 = x\sqrt{x^{2} + x + 1})
Comment faire cette fois-ci ?
comme ça à première vue faire apparaitre u'*rac(u) et un changement de variable dans le terme en plus -0,5*rac(u)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Mar 2013, 14:44
par chan79 » 08 Mar 2013, 14:44
tu peux remplacer le x devant la racine par
-\fra{1}{2})
et utilise ce qu'a mis jlb
-
Elise3
- Membre Naturel
- Messages: 17
- Enregistré le: 07 Mar 2013, 17:19
-
 par Elise3 » 08 Mar 2013, 17:45
par Elise3 » 08 Mar 2013, 17:45
j'ai un peu de mal pour trouver la bonne variable, j'ai essayé cos(t), sin(t)...
-
Erlinaewen
- Membre Naturel
- Messages: 27
- Enregistré le: 08 Fév 2013, 23:42
-
 par Erlinaewen » 08 Mar 2013, 18:17
par Erlinaewen » 08 Mar 2013, 18:17
Pose
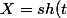)
,

réel, après avoir factorisé sous la racine avec
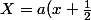)
,

étant à définir...
-
Elise3
- Membre Naturel
- Messages: 17
- Enregistré le: 07 Mar 2013, 17:19
-
 par Elise3 » 10 Mar 2013, 12:24
par Elise3 » 10 Mar 2013, 12:24
Erlinaewen a écrit:Pose
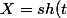)
,

réel, après avoir factorisé sous la racine avec
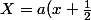)
,

étant à définir...
j'ai mis sous forme canonique :
^{2} + \frac{3}{4})
Et si j'ai bien compris...
 \leftrightarrow dx = ch(t))
Je suis sur la bonne voie ?
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 10 Mar 2013, 13:08
par jlb » 10 Mar 2013, 13:08
Elise3 a écrit:j'ai mis sous forme canonique :
^{2} + \frac{3}{4})
Et si j'ai bien compris...
 \leftrightarrow dx = ch(t))
Je suis sur la bonne voie ?
factorise d'abord par 3/4 sous la racine pour avoir un truce de la forme (ax+b)²+1 sous la racine et puis tu poses ax+b=sht
^{2} + 1})
après tu poses sht=2x/rac(3) + 1/rac(3)
-
Elise3
- Membre Naturel
- Messages: 17
- Enregistré le: 07 Mar 2013, 17:19
-
 par Elise3 » 10 Mar 2013, 17:58
par Elise3 » 10 Mar 2013, 17:58
j'y arrive pas :x
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
