Calcul de dm à partir de la masse m.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 02 Mar 2013, 14:29
par chelsea-asm » 02 Mar 2013, 14:29
Bonjour,
Je fais un exercice de Sciences de l'Ingénieur, mais ne trouvant pas de forum d'aide dans cette matière, je pense que cela se rapproche quand même pas mal des maths.
Je cherche l'opérateur d'inertie d'une plaque mince (donc d'épaisseur négligeable), de masse
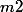
et de côté

selon

, et

selon

.
La formule de base, pour calculer un moment d'inertie est d'après mon cours :
 = \int_S (y^2 + z^2) dm)
Seulement je sais que la plaque a une masse m2, je n'ai pas la masse volumique.
Sachant que
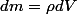
et
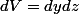
étant donné que

(épaisseur négligeable), comment calculer cette intégrale ne connaissant que la masse
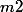
?
Est-ce possible ?
Merci pour vos réponses.
Cordialement.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 02 Mar 2013, 14:54
par Kikoo <3 Bieber » 02 Mar 2013, 14:54
Salut,
Normalement tu devrais avoir :
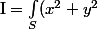\mathrm{d}m=\sigma \iint_{S}(x^2+y^2)\mathrm{d}x\mathrm{d}y)
avec
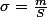
ce que l'on appelle la masse surface surfacique de ta plaque (qui a une épaisseur en x négligeable, donc pas besoin d'intégrer selon trois composantes)
Tu vas ensuite intégrer entre -a/2 et a/2, -b/2 et b/2. En fait le calcul du moment d'inertie se fait en sommant les masses de chaque point du solide fois sa distance au carré par rapport à l'axe (qui passe par le centre du rectangle homogène).
La première écriture ne sert pas à grand chose niveau calcul, sinon à simplifier la notation.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 02 Mar 2013, 15:07
par chelsea-asm » 02 Mar 2013, 15:07
Merci pour ta réponse, je comprends mieux la démarche ici.
En fait, le point où j'exprime le calcul est le centre d'inertie de la plaque mince.
Je pense qu'il n'y a donc pas à faire de rapport avec sa distance à un quelconque axe n'est-ce pas?
Pour ma part, j'ai essayé la méthode avec la masse surfacique donc, comme tu me l'as proposé, et au final je trouve que
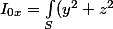 dydz = \frac{m2 a^2}{12} + \frac{m2 b^2}{12})
Après calculs en intégrant tour à tour en fonction de y et z entre -a/2 et a/2 puis -b/2 et b/2
où m2 est la masse de la plaque mince.
Qu'en penses-tu ?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 02 Mar 2013, 15:24
par Kikoo <3 Bieber » 02 Mar 2013, 15:24
chelsea-asm a écrit:Merci pour ta réponse, je comprends mieux la démarche ici.
En fait, le point où j'exprime le calcul est le centre d'inertie de la plaque mince.
Je pense qu'il n'y a donc pas à faire de rapport avec sa distance à un quelconque axe n'est-ce pas?
Pour ma part, j'ai essayé la méthode avec la masse surfacique donc, comme tu me l'as proposé, et au final je trouve que
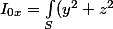 dydz = \frac{m2 a^2}{12} + \frac{m2 b^2}{12})
Après calculs en intégrant tour à tour en fonction de y et z entre -a/2 et a/2 puis -b/2 et b/2
où m2 est la masse de la plaque mince.
Qu'en penses-tu ?
C'est juste

Par contre j'aimerais relever un de tes commentaires :
Je pense qu'il n'y a donc pas à faire de rapport avec sa distance à un quelconque axe n'est-ce pas?
Si si, bien sûr ! Et c'est pour cela que l'on va intégrer entre -a/2 et a/2, ainsi que pour -b/2 et b/2
En fait, on considère que l'on se place au centre du rectangle, et que de là on va regarder la distance des autres points par rapport à soi. C'est de là d'où viennent les bornes d'intégration.
La distance d'un point par rapport à l'axe est désignée par le terme
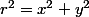
où r est cette distance.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 02 Mar 2013, 15:26
par chelsea-asm » 02 Mar 2013, 15:26
Kikoo <3 Bieber a écrit:C'est juste

Parfait

Merci pour ton aide !!!
Bonne journée, bon week-end !

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
