Complexe et fonction trigo
13 messages
- Page 1 sur 1
complexe et fonction trigo
Bonjour,
j'ai zn= [(sqrt3 +1)/4 +i(sqrt3 -1)/4]^n *(6+6i)
comment je peux calculer le module de zn ?
et pour un autre exercice :
f(x)=sin²x+sqrt(3)cosx
j'ai démontré que f(x)=f(-x)
la il faut montrer que pour tout x appartenant à (-pi/4;pi/4) on a 1.72<=f(x)<=1.75
et démontrer que l'équation f(x)=0 admet une unique solution dans l'intervalle (2;2.1)
Pouvez vous m'aider s'il vous plait ?
j'ai zn= [(sqrt3 +1)/4 +i(sqrt3 -1)/4]^n *(6+6i)
comment je peux calculer le module de zn ?
et pour un autre exercice :
f(x)=sin²x+sqrt(3)cosx
j'ai démontré que f(x)=f(-x)
la il faut montrer que pour tout x appartenant à (-pi/4;pi/4) on a 1.72<=f(x)<=1.75
et démontrer que l'équation f(x)=0 admet une unique solution dans l'intervalle (2;2.1)
Pouvez vous m'aider s'il vous plait ?
siger a écrit:Bonjour,
X = cosx
d'ou f(x) = -X²+V3*X +1
f'(x) = -2X+V3
je ne trouve pas cette relation, tu dis que cosx=-sinx ?
z_n s'écrit sous la forme d'un produit. Tu peux donc calculer les modules des différents facteurs de ton produits puis utiliser la propriété suivante : |ab|=|a|\times |b|
merci mais comment je fais pour la puissance ? je peux la sortir du module je crois ?
Salut !
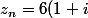 \( \frac{\sqrt 3 +1 }{4} + i \frac{\sqrt 3 -1 }{4} \)^n) .
.
Comme il t'a été dit plus haut, le module d'un produit, c'est le produit des modules donc :
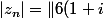 \( \frac{\sqrt 3 +1 }{4} + i \frac{\sqrt 3 -1 }{4} \)^n\|=6 |1+i|\times \| \( \frac{\sqrt 3 +1 }{4} + i \frac{\sqrt 3 -1 }{4} \)^n \| =6 |1+i|\times \| \frac{\sqrt 3 +1 }{4} + i \frac{\sqrt 3 -1 }{4} \| ^n) .
.
Tu as donc juste à calculer les modules :
 et
et 
Comme il t'a été dit plus haut, le module d'un produit, c'est le produit des modules donc :
Tu as donc juste à calculer les modules :
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
love-animo a écrit:je trouvepour l'autre
du coup ça me faispour le module de zn ?
Tout à fait !
Que l'on pourrait réécrire
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
love-animo a écrit:merci !!
c'est aussi égal à?
Non si tu mets un facteur
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
love-animo a écrit:pourtant je dois montrer que le module de zn est égal à ça
Oui c'est correct :++: (j'étais resté sur ma formule)
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
