Un exercice de math très beau

[simo_yassine]

a et b et c sont des nombre Entier relatif
soit que P(x)=ax²+bx+c
montre que si a et b et P(1) sont des nombres impairs
il n'ya pas de solution rationnel pour P(x)=0
avec justification

[tototo]

a et b et c sont des nombre Entier relatif
soit que P(x)=ax²+bx+c
montre que si a et b et P(1) sont des nombres impairs
il n'ya pas de solution rationnel pour P(x)=0
avec justification

bonjour

le produit de deux nombres impaires n'est pas un carre
(2n+1)*(2m+1)=4nm+2n+2m+1=4nm+2(n+m)+1=(a+b)^2
b=1 a=2(n+m)
or a^2=4nm different de 4(n+m)^2 donc ce n'est pas un carre donc la solution est irrationnel

[chan79]

bonjour

le produit de deux nombres impaires n'est pas un carre

bonjour
on a quand même 27*3=9²

[Archytas]

En effet joli problème, je dois avouer que j'ai mis du temps avant de trouver :we: !!
Tu veux de l'aide pour résoudre le problème ou tu as déjà la solution ?

[nodjim]

La seule difficulté, si on veut, consiste à prouver que la somme et le produit de 2 rationnels non entiers ne sont pas entiers tous les 2 à la fois.

[turfiste2012]

Bonjour,

que pensez-vous de:

-si p/q est solution alors nécessairement p²+pq+q² est pair

-cas p pair, q pair: on exclut car on veut que la fraction soit irréductible
-cas p pair, q impair alors p²+pq+q² impair (contradiction)
-cas p impair, q impair alors p²+pq+q² impair (contradiction)

A+

[Archytas]

La seule difficulté, si on veut, consiste à prouver que la somme et le produit de 2 rationnels non entiers ne sont pas entiers tous les 2 à la fois.

Je ne vois pas comment tu arrives là, j'imagine que tu utilise la forme x²-Sx+P mais pour identifier on devrait mettre le polynôme sous la forme , non ??
Et turfiste comme tu arrives au fait que p²+pq+q² est necessairement pair ?

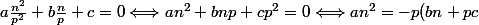Perso j'y suis aller par l'absurde si il existe une solution rationnelle alors il existe n et p premiers entre eux tels que : d'après Gauss p divise a donc p est impair, si n est pair à gauche le membre est pair et à droite il est impair et si n est impair à gauche il est impair et à droite il est pair. D'où les absurdités, donc n et p n'existent pas.

[turfiste2012]

a impair, b impair, a+b+c impair donc c impair

a=2u+1
b=2v+1
c=2w+1

p/q solution donne ap²+bpq+cq²=0

soit p²+pq+q² = -2(up²+vpq+wq²) donc p²+pq+q² pair

A+