Nombres complexes dans le plan

[NIniie]

Bonjour à tous, :we:

Je suis en terminale S et n'arrive pas à résoudre cet exercice sur les nombres complexes:

Soit les points A d'affixe i, B(-2i), D(1). E est le point tel que le triangle ADE soit équilatéral direct.
1) Démontrer que le point E a pour affixe (1/2-(;)3/2))(1+i)

J'ai tenter de calculer l'affixe à partir de l'argument et du module mais ca n'a pas marché et j'ai aussi essayer d'étudier les égalités vectorielles au sein du triangle mais là encore ca n'a rien donné de concret.

Bref, je vous demande votre aide. J'aimerais bien obtenir quelques pistes pour avancer.

Merci d'avance.

[Pixis]

Bonjour

Je n'ai pas fait les calculs, mais ya différentes manières de le faire
Soit tu fais un système tel que AD=DE et AD=AE
Soit tu fais un système tel que arg(AE-AD)=Pi/3 et arg(DE-DA)=Pi/3 également

J'espère que ces pistes d'aideront.

edit : Après calculs, tout est bon. Je te donne la trame de résolution de la première méthode :

Si on rapporte le plan complexe à un plan dans lR², et on donne E de coordonnées (x,y)
On a donc A(0,1) , D(1,0), E(x,y)
Donc les différents vecteurs suivant sont tels que
AD(1,-1)
DE(x-1,y)
AE(x,y-1)
On peut donc calculer les normes de ces différents vecteurs (qu'on met au carré pour simplifier les calculs)
llADll² = 2
llDEll² = (x-1)² + y² = x² + y² + 1 - 2x
llAEll² = (x-1)² + y² = x² + y² + 1 - 2y

On a donc le système suivant :

2 = (x-1)² + y² = x² + y² + 1 - 2x (1)
2 = (x-1)² + y² = x² + y² + 1 - 2y (2)

Par (1) et (2) on trouve que x=y
On remplace alors dans (1) y par x (par exemple)
On trouve une équation du second degré, avec delta>0 donc deux solutions réelles. Le choix de la bonne est déterminé par le fait que le triangle équilatéral l'est directement !

Bon courage

[chan79]

Bonjour à tous, :we:

Je suis en terminale S et n'arrive pas à résoudre cet exercice sur les nombres complexes:

Soit les points A d'affixe i, B(-2i), D(1). E est le point tel que le triangle ADE soit équilatéral direct.
1) Démontrer que le point E a pour affixe (1/2-(;)3/2))(1+i)

J'ai tenter de calculer l'affixe à partir de l'argument et du module mais ca n'a pas marché et j'ai aussi essayer d'étudier les égalités vectorielles au sein du triangle mais là encore ca n'a rien donné de concret.

Bref, je vous demande votre aide. J'aimerais bien obtenir quelques pistes pour avancer.

Merci d'avance.

salut
J'écrirais

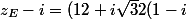[annick]

Bonjour,
ça me parait plus simple de raisonner avec module et argument.

Si AD=AE et angle (AD,AE)=-pi/3, cela se traduit par :

(zE-zA)/(zD-zA)=e^i(-pi/3)

D'où :

zE=zA+(zd-zA)(1/2-iV3/2)

Il ne reste plus qu'à finir le calcul et on trouve bien ce qui est demandé.

edit : encore un croisement, Chan79, et encore une fois d'accord. :lol3:

[NIniie]

Merci beaucoup pour vos réponses. Alors, j'ai compris la première méthode mais concernant la deuxième j'arrive pas trop a comprendre le principe: Pourquoi faire une égalité avec Pi/3?

[chan79]

Merci beaucoup pour vos réponses. Alors, j'ai compris la première méthode mais concernant la deuxième j'arrive pas trop a comprendre le principe: Pourquoi faire une égalité avec Pi/3?

Uploaded with ImageShack.us

[NIniie]

Ah, d'accord! Ca parait plus limpide tous de suite! Encore merci :)