hakka a écrit:peut tu m'aider pour la derniere question je suis vraiment bloqué je ne vois pas comment calculé cette limite a 10^-6 près
Je reformule :
Les suites (u_n) et (v_n) sont adjacentes et tendent vers la même limite :

Cette limite sera atteinte à

près si
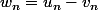
qui représente l'écart de
)
avec

est

ce qui est réalisé pour le rang n de développement de
)
tel que

ou

On ne peut pas résoudre simplement cette inéquation mais opérer par tâtonnements et en s'aidant d'une table donnant les premières factorielles :

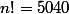
,
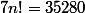

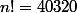
,
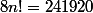

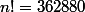
,
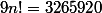
On voit donc qu'avec
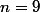
on approche

à moins de
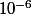
prés
Le calcul de

(j'avoue l'avoir trouvé tout fait sur un site) donne :
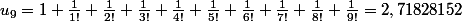
Si l'on compare à une valeur de e tronquée à 10 décimales : 2,7182818284, on vérifie que les 6 premières décimales coïncident. Preuve que l'on a bien approché e à
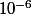
près.
Fin du feuilleton !
