Petit Exercice sur les dérivés

[darkode]

Bonjour bonsoir ,

ABC est un triangle équilatéral , longueur de AB = a .

- Déterminez la longueur et la largeur d'un rectangle dans le triangle et que son air soit la valeur maximal qu'elle peut prendre .

[Cheche]

Bonjour Darkode,

- Commences par faire un dessin pour savoir à quoi ressemble la figure.
- Si on considère que la largeur est x, quelle est la longueur du rectangle ?

[darkode]

Bonjour Darkode,

- Commences par faire un dessin pour savoir à quoi ressemble la figure.
- Si on considère que la largeur est x, quelle est la longueur du rectangle ?

Ehm d'après ce que j'ai trouvé auparavant , y = sin ( pi sur 3 ) * ( a - x )
Juste ?

[Cheche]

c'est presque ça.
Il y a une erreur sur le "( a - x )".

[Clu]

Pour moi c'est juste.

[Cheche]

Ah.

Pour ma part, j'ai mis le x horizontalement et le y verticalement.
Et tu obtiens que :



Effectivement, tu obtiens derrière que :



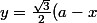Je pensais qu'il avait oublié le "/2".
Maintenant, il te suffit de déterminer quand la dérivée s'annule.

[darkode]

J'ai très bien fait jusque là , c'est juste au final , j'obtiens une incohérence .....

Est il possible de finir l'exercice ?

[darkode]

up . Personne :/ ? :hein:

[Clu]

On note f(x) l'aire du rectangle de largeur x. On a donc f(x) = x*y = x*sin(Pi/3)*(a-x)/2.
Tu dérives la fonction f et tu résous f'(x)=0. La valeur de x obtenue est la valeur pour laquelle l'aire du triangle est maximale.
Pour montrer rigoureusement qu'il s'agit d'un maximum il faut étudier les variations de f (que tu trouveras en étudiant le signe de la dérivée).