Limites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Rimchi
- Membre Naturel
- Messages: 49
- Enregistré le: 25 Nov 2012, 14:45
-
 par Rimchi » 16 Fév 2013, 17:25
par Rimchi » 16 Fév 2013, 17:25
Bonjour tout le monde,
Il faut que je compte la limite de cette fonction dans a :
(a=0) f(x) = ;)cosx - cos x / sin²x
Des idées?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 16 Fév 2013, 17:37
par Carpate » 16 Fév 2013, 17:37
Rimchi a écrit:Bonjour tout le monde,
Il faut que je compte la limite de cette fonction dans a :
(a=0) f(x) =

cosx - cos x / sin²x
Des idées?
Est-ce limite en 0 de

?
-
Rimchi
- Membre Naturel
- Messages: 49
- Enregistré le: 25 Nov 2012, 14:45
-
 par Rimchi » 16 Fév 2013, 17:49
par Rimchi » 16 Fév 2013, 17:49
Carpate a écrit:Est-ce limite en 0 de

?
Oui c'est bien celà

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Fév 2013, 17:54
par chan79 » 16 Fév 2013, 17:54
Rimchi a écrit:Oui c'est bien celà
salut
multiplie en haut et en bas par la quantité conjuguée du numérateur
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 16 Fév 2013, 18:18
par Carpate » 16 Fév 2013, 18:18
chan79 a écrit:salut
multiplie en haut et en bas par la quantité conjuguée du numérateur
Ca ne lève pas l'indétermination

En appliquant la règle de l'Hôpital on trouve
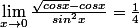
Mais ce n'est pas du niveau lycée ...

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Fév 2013, 18:26
par chan79 » 16 Fév 2013, 18:26
Carpate a écrit:Ca ne lève pas l'indétermination

En appliquant la règle de l'Hôpital on trouve
=\frac14)
Mais ce n'est pas du niveau lycée ...
}-cos(x)}{sin^2(x)}=\fra{cos(x)-cos^2(x)}{sin^2(x)(\sqrt{cos(x)}+cos(x))}=\fra{cos(x)(1-cos(x))}{4sin^2 (x/2) cos^2(x/2)(\sqrt{cos(x)}+cos(x))})
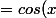2sin^2(x/2)}{4sin^2 (x/2) cos^2(x/2)(\sqrt{cos(x)}+cos(x))})
ça se simplifie et l'indétermination est levée
on trouve 1/4
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 16 Fév 2013, 18:28
par Carpate » 16 Fév 2013, 18:28
chan79 a écrit:}-cos(x)}{sin^2(x)}=\fra{cos(x)-cos^2(x)}{sin^2(x)(\sqrt{cos(x)}+cos(x))}=\fra{cos(x)(1-cos(x))}{4sin^2 (x/2) cos^2(x/2)(\sqrt{cos(x)}+cos(x))})
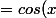2sin^2(x/2)}{4sin^2 (x/2) cos^2(x/2)(\sqrt{cos(x)}+cos(x))})
ça se simplifie et l'indétermination est levée
on trouve 1/4
C'est bien !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
