Géométrique analytique droites concourantes (ingénieur)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
LevraiDD
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Fév 2013, 11:46
-
 par LevraiDD » 13 Fév 2013, 13:15
par LevraiDD » 13 Fév 2013, 13:15
Bonjour,
Préparant actuellement une dispense d'ici 1 mois, je m'attèle à quelques exercices de géométrie analytique.
J'ai du mal à résoudre l'exercice dont voici l'énoncé:

Je ne sais pas si je dois vérifier que l'intersection de chacune des droites donne les mêmes coordonnées d'intersection, ou partir dans une résolution via les médianes ou médiatrices de constructions triangulaires ou autre,...
Dans n'importe quel cas, je ne sais pas si je dois poser des coordonnées en lettre et résoudre ou obtenir des caractéristiques pour les différentes droites et points découlant du fait que A(a,0) et B(0,b) sont connus...
Je sèche un peu.
Pourriez-vous m'éclairer?
Merci d'avance.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 13 Fév 2013, 15:14
par jlb » 13 Fév 2013, 15:14
LevraiDD a écrit:Bonjour,
Préparant actuellement une dispense d'ici 1 mois, je m'attèle à quelques exercices de géométrie analytique.
J'ai du mal à résoudre l'exercice dont voici l'énoncé:

Je ne sais pas si je dois vérifier que l'intersection de chacune des droites donne les mêmes coordonnées d'intersection, ou partir dans une résolution via les médianes ou médiatrices de constructions triangulaires ou autre,...
Dans n'importe quel cas, je ne sais pas si je dois poser des coordonnées en lettre et résoudre ou obtenir des caractéristiques pour les différentes droites et points découlant du fait que A(a,0) et B(0,b) sont connus...
Je sèche un peu.
Pourriez-vous m'éclairer?
Merci d'avance.
Bonjour, ( si le repère est orthonormé!!!)
équation de (AB): x/a + y/b = 1
yD = u*xD et yC = u*xC
en utilisant le produit scalaire ( en coordonnées + projection): OC² =b*yC et OD² = a*xD
Vérifie alors que le point de coordonnées ( xD;yC) appartient à (AB) ( quelques petits calculs en utilisant toutes les relations précédentes)
Bon courage

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 14 Fév 2013, 08:35
par chan79 » 14 Fév 2013, 08:35
Bonjour
[img]
[IMG]http://img850.imageshack.us/img850/5424/33735132.gif[/img]Ce n'est pas mieux que par l'analytique, mais on peut aussi utiliser la propriété de Thalès:
A et B se projettent sur
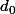
en C et D.
(AB) et
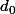
se coupent en E.La droite

, perpendiculaire à Ox passant par D, coupe (AB) en F.
On trace (en rouge) la droite (CF) et il faut donc démontrer qu'il s'agit de la droite

, c'est à dire qu'elle est parallèle à Ox.
D'après la propriété de Thalès


A partir des produits en croix, on a EA. EC=EO.EF
donc

ce qui prouve que la droite rouge est bien parallèle à Ox et que c'est bien la droite

de l'énoncé.

,

et (AB) sont concourantes en F.
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 14 Fév 2013, 10:58
par Maxmau » 14 Fév 2013, 10:58
LevraiDD a écrit:Bonjour,
Préparant actuellement une dispense d'ici 1 mois, je m'attèle à quelques exercices de géométrie analytique.
J'ai du mal à résoudre l'exercice dont voici l'énoncé:

Je ne sais pas si je dois vérifier que l'intersection de chacune des droites donne les mêmes coordonnées d'intersection, ou partir dans une résolution via les médianes ou médiatrices de constructions triangulaires ou autre,...
Dans n'importe quel cas, je ne sais pas si je dois poser des coordonnées en lettre et résoudre ou obtenir des caractéristiques pour les différentes droites et points découlant du fait que A(a,0) et B(0,b) sont connus...
Je sèche un peu.
Pourriez-vous m'éclairer?
Merci d'avance.
Bonjour
une autre façon
la droite (BC) coupe (OX) en E
la droite (OY) coupe d1 en F
p la projection orthogonale de (OX) sur d0 (c'est une bijection affine de (OX) sur d0)
q la projection orthogonale de d0 sur d1
la composée de ces 2 projections r = qop est une bijection affine de (OX) sur d1
D'autre part r(E) = C et r(O) = F
r est donc la projection centrale de centre B de (OX) sur d1
conc: A , r(A) et B sont donc alignés
-
Black Jack
 par Black Jack » 14 Fév 2013, 12:29
par Black Jack » 14 Fév 2013, 12:29
Et en "analytique", comme demandé dans le titre :
do : y = kx.
C(X1 ; kx1)
B(0 ; b)
vect BC (X1 ; kX1-b)
vect(OC) . vect(BC) = 0
X1² + .kX1(k.X1-b) = 0
et comme X1 est diff de 0 --->
X1 + k(k.X1-b) = 0
X1(1+k²) - kb = 0
X1 = k.b/(1+k²)
D(X2 ; kx2)
A(a ; 0)
vect AD (X2-a ; kX2)
vect(OD) . vect(AD) = 0
X2(X2-a) + k²X2² = 0
et comme X2 est diff de 0 --->
X2-a + k²X2 = 0
X2 = a/(1+k²)
d2 : x = a/(1+k²)
d1 : y = k².b/(1+k²)
(AB) : y = -(b/a)x + b
Le point de rencontre de d1 et d2 est P(a/(1+k²) ; k².b/(1+k²))
d1, d2 et (AB) sont coucourantes si les coordonnées de P satisfont l'équation de (AB).
Vérifions, si c'est le cas :
k².b/(1+k²) =? -(b/a).a/(1+k²) + b
k².b/(1+k²) =? -b/(1+k²) + b
k².b/(1+k²) =? b(-1+1+k²)/(1+k²)
k².b/(1+k²) =? k²b/(1+k²) C'est OK
Et donc d1, d2 et (AB) sont coucourantes.
:zen:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 14 Fév 2013, 13:00
par chan79 » 14 Fév 2013, 13:00
Maxmau a écrit:D'autre part r(C) = E et r(F) = O
c'est pas r(E)=C ?
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 14 Fév 2013, 13:06
par Maxmau » 14 Fév 2013, 13:06
chan79 a écrit:c'est pas r(E)=C ?
Bj
Oui tu as raison
r(E)=C et r(O)=F je vais corriger
merci
-
LevraiDD
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Fév 2013, 11:46
-
 par LevraiDD » 14 Fév 2013, 14:24
par LevraiDD » 14 Fév 2013, 14:24
Merci à tous pour vos différents développements et l'efficacité!
J'y vois plus clair maintenant.
Bonne fin de journée à tous ;)
-
LevraiDD
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Fév 2013, 11:46
-
 par LevraiDD » 14 Fév 2013, 22:16
par LevraiDD » 14 Fév 2013, 22:16
Je suis allé un peu vite.
Black Jack, comment peux-tu affirmer que l'ordonnée de OC et celle de OD on le même coefficient multiplicateur k?
Cette manière est elle la seule voie de résolution par l'analytique?
-
Black Jack
 par Black Jack » 15 Fév 2013, 08:21
par Black Jack » 15 Fév 2013, 08:21
LevraiDD a écrit:Je suis allé un peu vite.
Black Jack, comment peux-tu affirmer que l'ordonnée de OC et celle de OD on le même coefficient multiplicateur k?
Cette manière est elle la seule voie de résolution par l'analytique?
Une droite passant par l'origine du repère (et non parallèle à l'axe des ordonnée) a pour équation:
y = k.x
Tout point de cette droite a donc des coordonnées (X ; kX), X étant l'abscisse du point.
La droite (CD) passe par l'origine du repère et son équation est donc y = k.x (avec k un réel)
les points C et D sont donc repérés par C(X1 ; kX1) et D(X2 ; kX2), X1 étant l'abscisse du point C et X2 étant l'abscisse du point C2.
:zen:
-
LevraiDD
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Fév 2013, 11:46
-
 par LevraiDD » 15 Fév 2013, 10:56
par LevraiDD » 15 Fév 2013, 10:56
Yes juste! A force, j'en oublie les choses simples de base ;)
Merci pour ton aide, c'est parfait!
Bonne journée
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités

