[L2] Convergence en loi.

[Deluxor]

Bonjour à tous,

Je voudrais démontrer ce résultat :


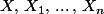
Soit des variables aléatoires à valeurs dans .
Montrer que :


Je suppose devoir utiliser la définition de mon cours ; c'est-à-dire :

.

Je ne vois pas comment facilement déduire le résultat.


Je vous remercie,

Deluxor

[DamX]

Bonjour à tous,

Je voudrais démontrer ce résultat :


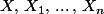
Soit des variables aléatoires à valeurs dans .
Montrer que :


Je suppose devoir utiliser la définition de mon cours ; c'est-à-dire :

.

Je ne vois pas comment facilement déduire le résultat.


Je vous remercie,

Deluxor

Bonjour,

Que vaut ?

Damien

[Deluxor]

Bonsoir Damien,



Ainsi :

[DamX]

Bonsoir Damien,



Ainsi :

Oui mais je voyais plutôt d'utiliser ce resultat pour exprimer de deux manières différentes..