Vecteurs aléatoires, matrice de rang 1
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
marievlan
- Membre Naturel
- Messages: 19
- Enregistré le: 26 Sep 2012, 18:11
-
 par marievlan » 11 Fév 2013, 19:04
par marievlan » 11 Fév 2013, 19:04
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Fév 2013, 19:31
par Doraki » 11 Fév 2013, 19:31
c'est dans quel sens que tu n'y arrives pas ?
-
lefokisetouf
- Membre Naturel
- Messages: 20
- Enregistré le: 17 Juil 2008, 14:50
-
 par lefokisetouf » 12 Fév 2013, 17:30
par lefokisetouf » 12 Fév 2013, 17:30
Bonjour,
Nous sommes dans la même classe et c'est la réciproque que nous ne parvenons pas à démontrer...
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 12 Fév 2013, 19:39
par Doraki » 12 Fév 2013, 19:39
Donc tu supposes que la matrice P(X = xi, Y = yj) est de rang 1,
et tu cherches à montrer qu'il existe p+q réels P(X=xi), P(Y = yj) tels que P(X = xi, Y = yj) = P(X=xi)*P(Y=yj).
Tout d'abord, comme peut-on "lire" les valeurs de P(X=xi) et de P(Y=yj) sur ta matrice ?
-
lefokisetouf
- Membre Naturel
- Messages: 20
- Enregistré le: 17 Juil 2008, 14:50
-
 par lefokisetouf » 12 Fév 2013, 20:54
par lefokisetouf » 12 Fév 2013, 20:54
Euh... bonne question ...
C'est là tout le problème : on ne voit pas comment faire "ressortir" les P(X=xi) et P(Y=yj) alors qu'il n'y a que des P(X=xi,Y=yj)...
-
marievlan
- Membre Naturel
- Messages: 19
- Enregistré le: 26 Sep 2012, 18:11
-
 par marievlan » 13 Fév 2013, 12:48
par marievlan » 13 Fév 2013, 12:48
En sommant les valeurs sur une ligne de la matrice, on obtient [TEX]\mathbb{P}(X=x_i)[\TEX] et en sommant les valeurs des colonnes, on obtient [TEX]\mathbb{P}(Y=y_i)[\TEX]. C'est ça non ?
Mais après comment en déduire ce qu'on veut ?
-
marievlan
- Membre Naturel
- Messages: 19
- Enregistré le: 26 Sep 2012, 18:11
-
 par marievlan » 13 Fév 2013, 12:48
par marievlan » 13 Fév 2013, 12:48
En sommant les valeurs sur une ligne de la matrice, on obtient
)
et en sommant les valeurs des colonnes, on obtient
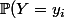)
. C'est ça non ?
Mais après comment en déduire ce qu'on veut ?
-
hamza-Topo
- Messages: 1
- Enregistré le: 13 Fév 2013, 13:04
-
 par hamza-Topo » 13 Fév 2013, 13:24
par hamza-Topo » 13 Fév 2013, 13:24
C'est là tout le problème : on ne voit pas comment faire "ressortir" les P(X=xi) et P(Y=yj) alors qu'il n'y a que des P(X=xi,Y=yj)...
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 13 Fév 2013, 15:13
par Doraki » 13 Fév 2013, 15:13
marievlan a écrit:En sommant les valeurs sur une ligne de la matrice, on obtient
)
et en sommant les valeurs des colonnes, on obtient
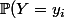)
. C'est ça non ?
Mais après comment en déduire ce qu'on veut ?
Oui.
Que peux-tu dire des vecteurs colonnes de la matrice et de la colonne (P(X=xi)) (qui est donc la somme des vecteurs colonnes de la matrice) ?
-
marievlan
- Membre Naturel
- Messages: 19
- Enregistré le: 26 Sep 2012, 18:11
-
 par marievlan » 13 Fév 2013, 16:55
par marievlan » 13 Fév 2013, 16:55
Doraki a écrit:Oui.
Que peux-tu dire des vecteurs colonnes de la matrice et de la colonne (P(X=xi)) (qui est donc la somme des vecteurs colonnes de la matrice) ?
Oui, j'ai remarqué que les colonnes (et les lignes) sont linéairement dépendantes. Il existe donc un vecteur
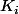
tel que toutes les colonnes
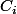
peuvent s'exprimer comme

On utilise le fait que les lignes sont lin. dépendantes aussi.
On obtient donc :
 = \mathbb{P}(X=x_i, Y=y_1) \times k)
où k est un scalaire.
De même, on a :
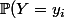 = \mathbb{P}(X=x_1, Y=y_i) \times l)
où l est un scalaire.
Mais je n'arrive pas à conclure !!!!
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 13 Fév 2013, 22:19
par Doraki » 13 Fév 2013, 22:19
Et le vecteur colonne (P(Xi)) comparé aux autres vecteurs colonnes ?
A un moment tu auras besoin de dire que la somme de toutes les probabilités dans la matrice vaut 1.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
et en sommant les valeurs des colonnes, on obtient
. C'est ça non ?