Limites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nelson
- Messages: 2
- Enregistré le: 14 Aoû 2006, 12:20
-
 par nelson » 14 Aoû 2006, 12:22
par nelson » 14 Aoû 2006, 12:22
bonjour j'ai cet exo que je n'arrive pas à faire:
Déterminer les limites suivantes aux bornes de l'ensemble de définition:
1)f(x)= -X²+3X-5
2)g(x)=[-x^2+5x+4]/x-2
3)h(x)= [racine de(x²-2x-x) ]-x
help me please!
merci d'avance j'espère avoir été assez clair pour écrire l'énoncée
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Aoû 2006, 12:25
par Nightmare » 14 Aoû 2006, 12:25
Bonjour
tu peux regarder
cette page
-
euclide
- Membre Relatif
- Messages: 100
- Enregistré le: 10 Aoû 2006, 13:22
-
 par euclide » 14 Aoû 2006, 13:26
par euclide » 14 Aoû 2006, 13:26
N'oubli pas pour ton exercice de d'abord trouver les différents ensembles de définitions et donc les éventuelles valeurs interdites. C'est pas toujours en + ou - l'infini. Ensuite utilise les propriétés correspondantes qu'il y a dans le lien précédent.
-
nelson
- Messages: 2
- Enregistré le: 14 Aoû 2006, 12:20
-
 par nelson » 17 Aoû 2006, 08:44
par nelson » 17 Aoû 2006, 08:44
voila j'essay le premier:
1)f(x)= -X²+3X-5
lim(x>oo) 3x-5= oo
et lim -X²=-oo
donc d'après mon petit tableau on ne peut conclure pour lim(fx)
non?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 17 Aoû 2006, 10:29
par fonfon » 17 Aoû 2006, 10:29
salut,
voila j'essay le premier:
1)f(x)= -X²+3X-5
lim(x>oo) 3x-5= oo
et lim -X²=-oo
donc d'après mon petit tableau on ne peut conclure pour lim(fx)
non?
je sais pas tu es en quelle classe?
sinon
}=-x^2+3x-5)
Df=R=]-inf,+inf[
donc on va mettre le terme de plus haut degré en facteur soit x² donc
}=x^2(-1+\frac{3}{x}-\frac{5}{x^2}))
et
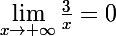
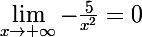
et
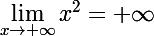
mais comme il reste le -1 on a donc
}=-\infty)
essaies de faire la limite en -inf
ps: avec la cours de Nightmare tu devrais t'en sortir
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 17 Aoû 2006, 10:29
par nada-top » 17 Aoû 2006, 10:29
bonjour
la limite en l'infini
)
d'une fonction polynôme

la limite de son monôme du plus haut degré.
pour 1)
= -x^2+3x-5)
; donc
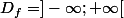
(fonction polnôme)
donc :
=\lim_{x \to +\infty}(-x^2)=-\infty)
=\lim_{x \to -\infty}(-x^2)=-\infty)
voilà en général :
= a_n x^n+ a_{n-1} x^{n-1}+....+a_1 x+a_0 \; (a_n \neq 0))
(le monôme du plus haut degré c
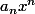
) comment déterminer sa limite en
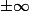
?
- la limite en

de
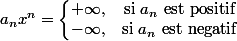
- la limite en

de
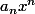
est :


@+
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 17 Aoû 2006, 10:32
par nada-top » 17 Aoû 2006, 10:32
bonjour fonfon désolée ..j'ai pas remarqué ton message.mais en tous cas il a maintenant une regle générale.
@+
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 17 Aoû 2006, 10:32
par fonfon » 17 Aoû 2006, 10:32
Salut nada-top, je pense que tu as fais une petite erreur car
}=-\infty)
A+
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 17 Aoû 2006, 10:36
par nada-top » 17 Aoû 2006, 10:36
ah oui j'ai pas fais attention. c'est réglé maintenant :we:
-
Mahdi
- Membre Naturel
- Messages: 29
- Enregistré le: 12 Nov 2005, 13:36
-
 par Mahdi » 17 Aoû 2006, 13:37
par Mahdi » 17 Aoû 2006, 13:37
L'ensemble de definition de g est

Alors la limite de g quand x tends vers

est la limite du quotient

c'est -oo
En suivant la meme methode on trouve que la limite a -oo est +oo
la limite quand x tends vers 2 :
si x>2 alors la limite de g est +oo
si x<2 alors la limite de g est -oo
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
}=-x^2+3x-5) Df=R=]-inf,+inf[
Df=R=]-inf,+inf[}=x^2(-1+\frac{3}{x}-\frac{5}{x^2}))
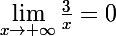
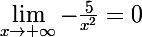
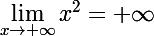
}=-\infty)
